3  Results

3.1 Regeneration

3.1.1 Basal area

Composition of regeneration in terms of basal area per acre represented by each species in a 4-meter radius vegetation plot was modeled as a gamma distribution with a log link with fixed effects for treatment and species, and random intercepts for site x species interaction. Dispersion was modeled separately as a function of species, using a log link and the rate of zeros was modeled using the logit link, for each species as well (Listing 3.1).

Listing 3.1 
Family: Gamma (log) 
Conditional: ba_ha ~ treat * spp + (1 | site:spp)  
Dispersion: ~spp (log) 
Hurdle: ~spp (logit)

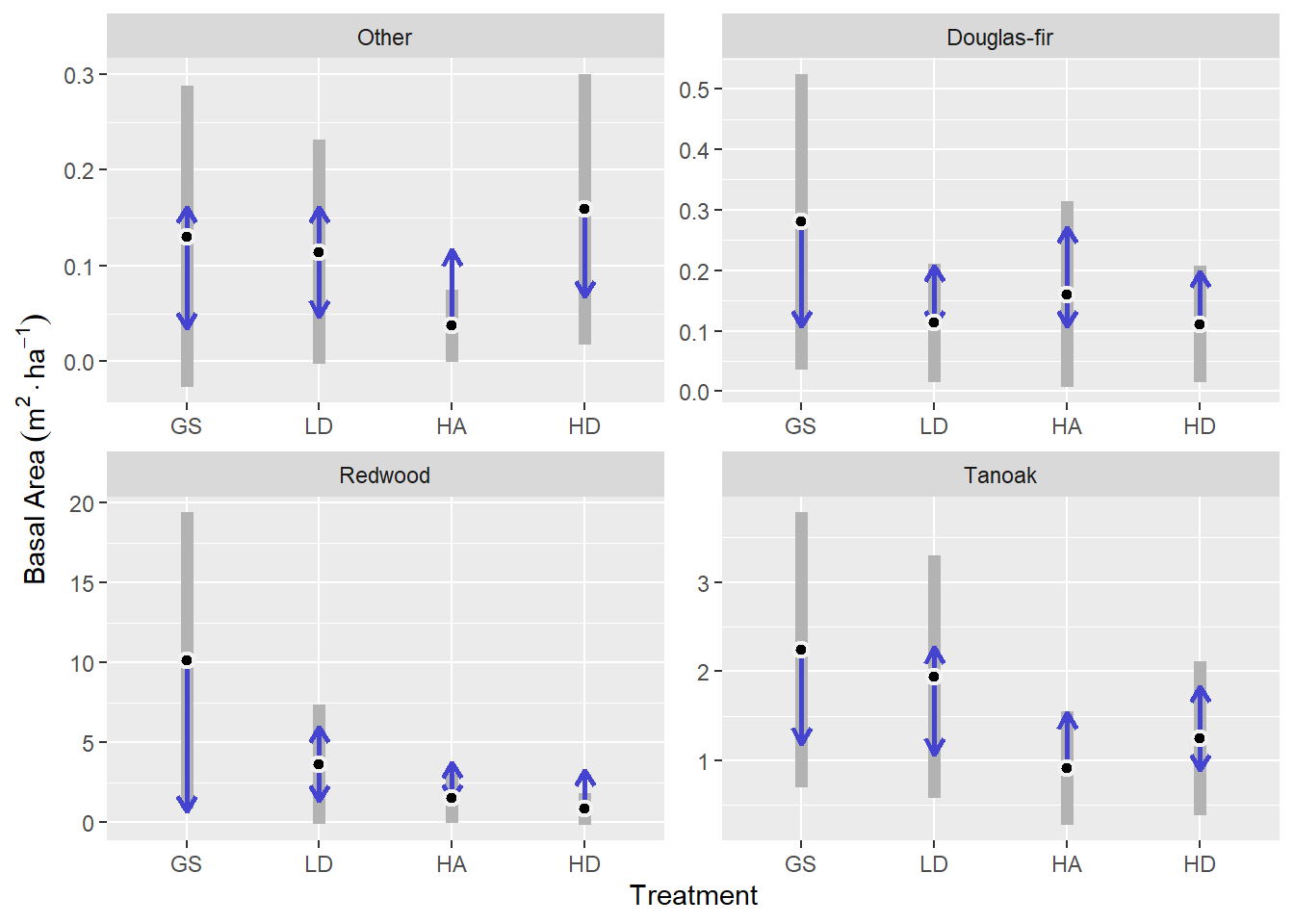
Focal species for this model included redwood, tanaok, Douglas-fir, and other species.

Redwood basal area regeneration showed the greatest treatment response. Where the GS treatment had the greatest basal area of redwood regeneration at m2 ha-1, which was 9.28 m2 ha-1 greater than in the HD treatment (p = 0.19). The LD and HD treatments were intermediate.

Tanoak basal area regeneration was intermediate between that of redwood and Douglas-fir and other species. The GS and LD treatments had similar responses, as did the HA and HD treatments. The GS treatment resulted in 2.24 m2 ha-1 of tanoak basal area, which was 1.33 m2 ha-1 greater than in the HA treatment (p = 0.18).

On average, for Douglas-fir, we expect about 0.17 m2 ha-1 of basal area across treatments. The greatest basal area of Douglas-fir was in the GS treatment which was 0.12 m2 ha-1 greater than in the HA treatment (p = 0.76). The LD, HA, and HD treatments were all comparatively similar.

Other species included grand fir, madrone, and California wax-myrtle, of which there was a total of 23, 28, and 16 observations across our 16 macro plots (comprising 64 tree density plots). Generally, each plot had between 0 and 9 observations of other species, except for one macro plot with the LD treatment, which had 16 observations (data not shown).

According to predictions made from this model for other species, there was not enough evidence to confirm a statistically significant difference between treatments. On average, we expect about 0.11 m2 ha-1 of basal area across treatments. The greatest basal area of other species was in the HD treatment which was 0.12 m2 ha-1 greater than in the HA treatment (p = 0.26). The GS and LD treatments were intermediate.

Table 3.1: Grand means (m2 ha-1) for basal area of regeneration of each species across treatments 10 years after the initiation of a multi-age redwood forest. The asymptotic 95% confidence intervals are based on the normal approximation.
Spp 1 Emmean SE DF 95% LCL 95% UCL
other overall 0.11 0.04 Inf 0.03 0.19
df overall 0.17 0.06 Inf 0.05 0.28
rw overall 4.03 1.52 Inf 1.04 7.01
to overall 1.59 0.47 Inf 0.67 2.50
Figure 3.1: Basal area (m2 ha-1) modeled at the vegetation plot level for four harvest treatments and four species classes (n = 16). Gray bars represent the 95% confidence interval (α = 0.05), black dots indicate the mean, and blue arrows provide a means of assessing the statistical significance of pairwise differences among treatments. Arrows are drawn so that when two arrows just meet, the p-value for that difference is 0.05 and overlapping arrows indicate a p-values greater than 0.05.
Table 3.2: Basal area (m2 ha-1) modeled at the vegetation plot level for four harvest treatments and four species classes (n = 16). The asymptotic 95% confidence intervals are based on the normal approximation.
Spp treatment Emmean SE DF 95% LCL 95% UCL
other gs 0.13 0.08 Inf -0.03 0.29
other ld 0.11 0.06 Inf -0 0.23
other ha 0.04 0.02 Inf -0 0.07
other hd 0.16 0.07 Inf 0.02 0.3
df gs 0.28 0.12 Inf 0.04 0.52
df ld 0.11 0.05 Inf 0.02 0.21
df ha 0.16 0.08 Inf 0.01 0.31
df hd 0.11 0.05 Inf 0.01 0.21
rw gs 10.12 4.74 Inf 0.84 19.41
rw ld 3.63 1.91 Inf -0.12 7.38
rw ha 1.51 0.78 Inf -0.01 3.04
rw hd 0.85 0.52 Inf -0.17 1.86
to gs 2.24 0.79 Inf 0.7 3.79
to ld 1.94 0.69 Inf 0.58 3.3
to ha 0.92 0.33 Inf 0.28 1.56
to hd 1.25 0.44 Inf 0.39 2.11
Table 3.3: Pairwise comparisons of treatments within species. P-values were adjusted using the Tukey method for comparing families of four estimates and they are based on large-sample (asymptotic) normal approximations.
Spp Contrast Emmean SE DF P value
other gs - ld 0.02 0.09 Inf 1
other gs - ha 0.09 0.08 Inf 0.6
other gs - hd -0.03 0.09 Inf 0.99
other ld - ha 0.08 0.06 Inf 0.53
other ld - hd -0.04 0.07 Inf 0.91
other ha - hd -0.12 0.07 Inf 0.26
df gs - ld 0.17 0.11 Inf 0.46
df gs - ha 0.12 0.12 Inf 0.76
df gs - hd 0.17 0.11 Inf 0.42
df ld - ha -0.05 0.08 Inf 0.93
df ld - hd 0 0.05 Inf 1
df ha - hd 0.05 0.07 Inf 0.91
rw gs - ld 6.49 4.6 Inf 0.49
rw gs - ha 8.61 4.56 Inf 0.23
rw gs - hd 9.28 4.64 Inf 0.19
rw ld - ha 2.12 1.8 Inf 0.64
rw ld - hd 2.79 1.83 Inf 0.42
rw ha - hd 0.67 0.79 Inf 0.83
to gs - ld 0.31 0.69 Inf 0.97
to gs - ha 1.33 0.65 Inf 0.18
to gs - hd 0.99 0.64 Inf 0.4
to ld - ha 1.02 0.58 Inf 0.29
to ld - hd 0.69 0.57 Inf 0.63
to ha - hd -0.33 0.37 Inf 0.8

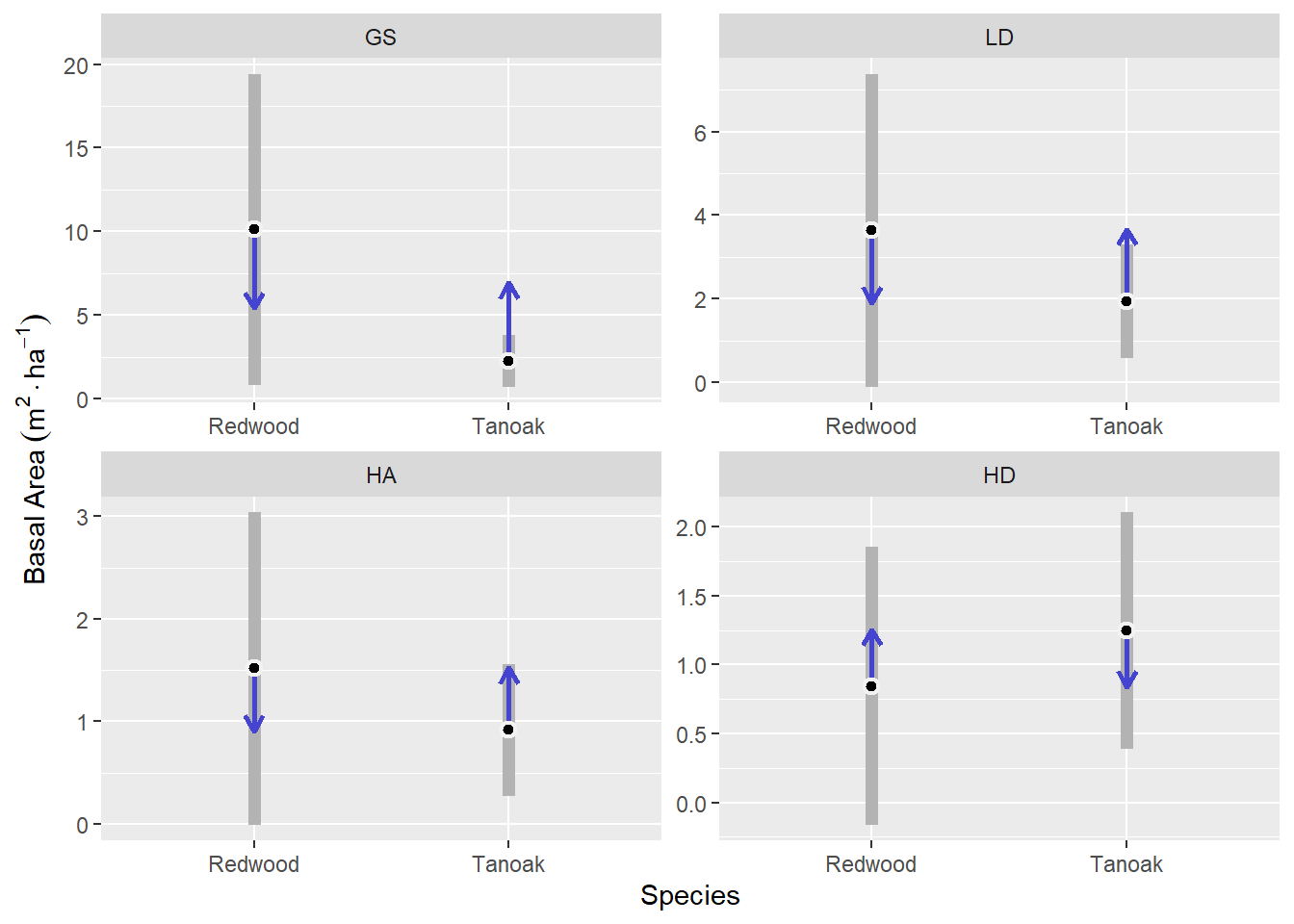
Figure 3.2 shows the same model as Figure 3.1, but with an emphasis on treatment comparisons between redwood and tanoak. This shows that we expect on average, 7.88 m2 ha-1 greater redwood basal area than tanoak basal area in the GS treatment (p = 0.1), about 1.69 m2 ha-1 in the LD treatment (p = 0.4), and about 0.6 m2 ha-1 in the HA treatment (p = 0.48). In the HD treatment, we expect to see slightly higher tanoak basal area (p = 0.55).

Uncertainty in average Redwood basal area across sites, indicated by the size of 95% confidence intervals, is much greater than that of tanoak in the GS treatment, but this difference diminishes such that GS > LD > HA > HD. In the HD treatment redwood and tanoak average basal area uncertainty across sites is very similar. (Figure 3.2).

Figure 3.2: Basal area (m2 ha-1) modeled at the vegetation plot level for four harvest treatments and two species classes (n = 16). Gray bars represent the 95% confidence interval, black dots—the mean, and non-overlapping blue arrows signify statistical significance (α = 0.05).

3.1.2 Douglas-fir counts

Counts of regenerating Douglas-fir seedlings per vegetation plot were analyzed for differences between harvest treatments using a negative binomial response with a log link, fixed effects for treatment, random effects for site and site x treatment interaction (Listing 3.2).

Listing 3.2 
Family: nbinom1 (log) 
Conditional: n ~ treat + (1 | site) + (1 | site:treat)

This model for Douglas-fir counts does not indicate any statistically significant differences between treatments. Generally, we expect about 2 seedlings per 4-meter-radius plot, or about 413 seedlings per hectare (Figure 3.3).

Figure 3.3: Vegetation plot level counts of regenerating Douglas-fir seedlings in four harvest treatments 10 years after harvest (n = 16). Results have been scaled to stems per hectare (4-meter radius plots). The asymptotic 95% confidence intervals are based on the normal approximation.
Table 3.4: Vegetation plot level counts of regenerating Douglas-fir seedlings in four harvest treatments 10 years after harvest (n = 16). Results have been scaled to stems per hectare from 4-meter radius plots. The asymptotic 95% confidence intervals are based on the normal approximation.
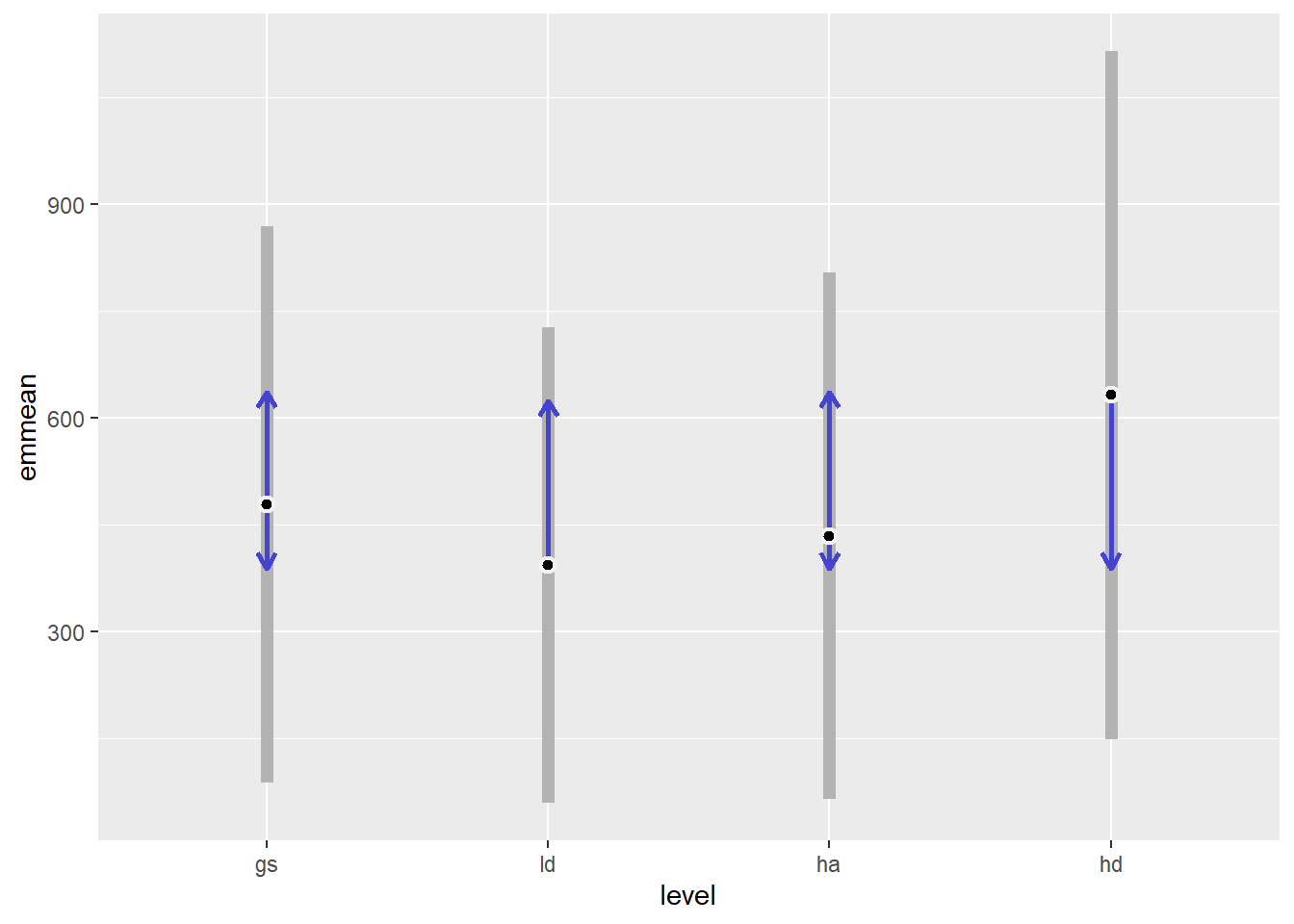
Treatment estimate asymp.LCL asymp.UCL
gs 479 88 869
ld 394 60 728
ha 435 65 805
hd 632 149 1115

3.2 Sprout heights

3.2.1 Height increment

The selected height increment model used a normal response distribution on the identity link. It included treatment, growth period, species, and the interaction of species and growth period as fixed effects. A random intercept was included for tree (multiple observations) and macro-plot, and an another random effect allowed the response to vary by species differently for each macro plot. The dispersion parameter for the response was modeled (with a log link) as a function of treatment, growth period, species and all three-way interactions (Listing 3.3).

Listing 3.3 
Family: gaussian (identity) 
Conditional: ht_inc ~ treat + year * spp + (1 | tree) + (0 + spp | plot)  
Dispersion: ~spp * year * treat (log)

The model selected based on AIC lacks a treatment x species interaction, suggesting that there is not evidence that treatments affected species differentially. It also lacks a treatment x year interaction. This means that there was not enough evidence to support that treatment was related to changes in growth rate.

The inclusion of treatment factors in the model (0.001 ≤ p < 0.03) indicated that the levels of treatment were associated with different growth rates across species and years. And the species x year interaction (p < 0.001) suggested that changes in growth rates were different for redwood and tanoak (Figure 3.4).

For tanoak, height increment was greatest in the GS treatment at 0.48 m yr-1. This was about 0.17 m yr-1 more than in the HA and HD treatments, which were very similar at about 0.3 m yr-1.

Redwood followed a similar pattern but with more pronounced differences between treatments. Height increment for redwood in the GS treatment was 0.96 m yr-1, which was about 0.4 m yr-1 greater than in the HD treatment (p = 0). Additionally, there was evidence that the GS treatment led to greater height increment than the LD treatment by about 0.17 m yr-1 (p = 0). And the LD treatment was higher than the HA treatment by about 0.15 m yr-1 (p = 0).

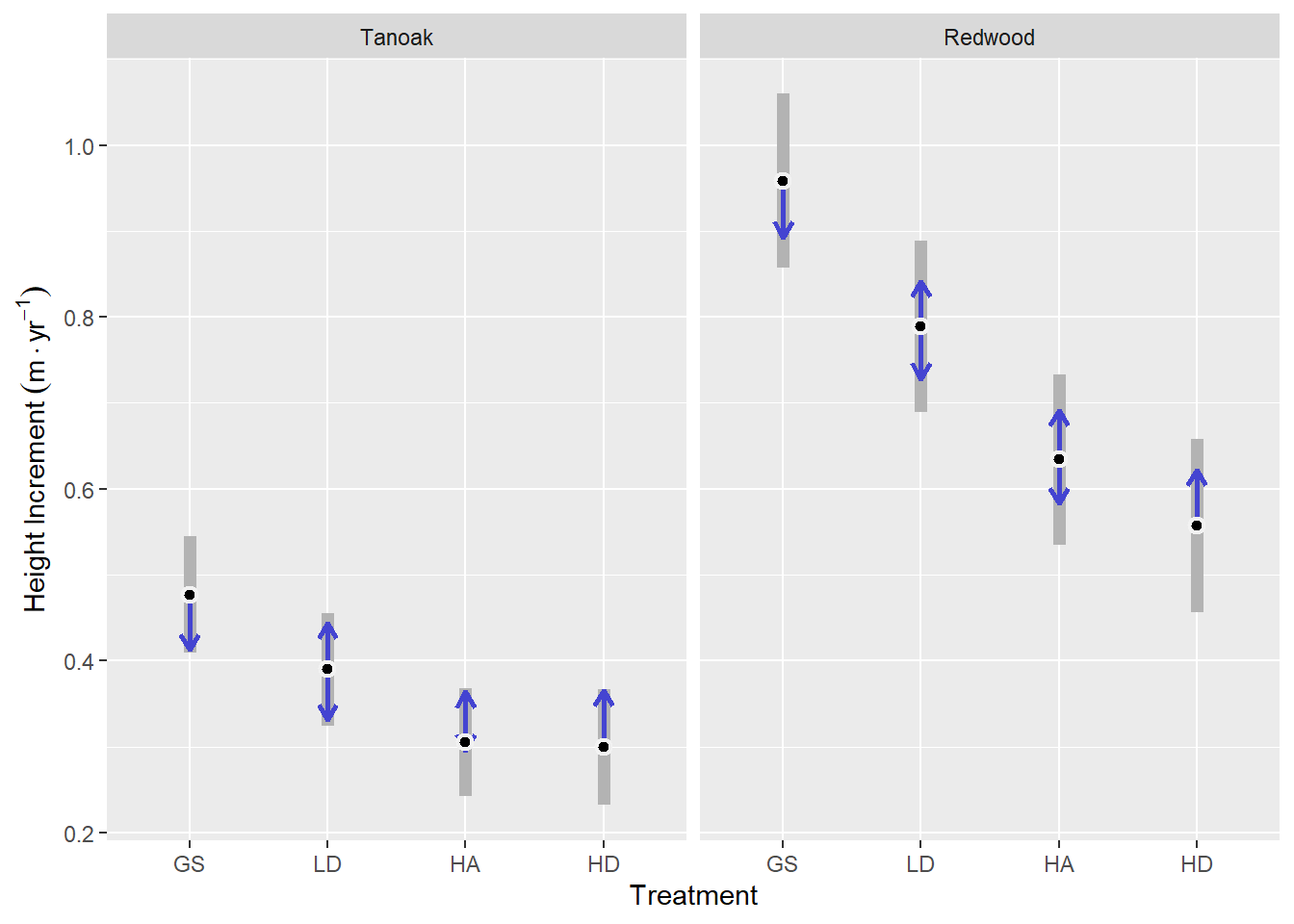
Figure 3.4: Estimated marginal means for the effect of harvest treatment on redwood and tanoak sprout height increment, averaged over two growth periods, ten years after harvest. Gray bars represent confidence intervals and statistical significance (α = 0.05) is indicated by non-overlapping blue arrows.
Table 3.5: Estimated marginal means for the effect of harvest treatment on redwood and tanoak sprout height increment, averaged over two growth periods, ten years after harvest. The asymptotic 95% confidence intervals are based on the normal approximation.
spp treatment estimate SE df asymp.LCL asymp.UCL
LIDE GS 0.48 0.034 Inf 0.41 0.54
LIDE LD 0.39 0.033 Inf 0.32 0.46
LIDE HA 0.31 0.032 Inf 0.24 0.37
LIDE HD 0.3 0.034 Inf 0.23 0.37
SESE GS 0.96 0.052 Inf 0.86 1.06
SESE LD 0.79 0.051 Inf 0.69 0.89
SESE HA 0.63 0.05 Inf 0.54 0.73
SESE HD 0.56 0.052 Inf 0.46 0.66

Redwood growth slowed from 0.80 to 0.67 m yr-1 in the second period and tanoak slowed from 0.39 to 0.34 m yr-1.

Redwood grew faster than tanoak, but slowed down more relative to it in the second period. Height increment for redwood was 0.42 m yr-1 greater than tanoak in the first period and 0.33 m yr-1 greater than tanoak in the second period (Figure 3.5).

Figure 3.5: Estimated marginal means for the effect of growth period on redwood and tanoak sprout height increment, averaged over four harvest treatments, from years 1 to 5, and years 5 to 10 after harvest, plotted alongside actual data. Gray bars represent confidence intervals and statistical significance (α = 0.05) is indicated by non-overlapping blue arrows.
Table 3.6: Estimated marginal means for the effect of growth period on redwood and tanoak sprout height increment, averaged over four harvest treatments, from years 1 to 5, and years 5 to 10 after harvest. The asymptotic 95% confidence intervals are based on the normal approximation.
spp year estimate SE df asymp.LCL asymp.UCL
LIDE 5 0.39 0.017 Inf 0.35 0.42
LIDE 10 0.35 0.017 Inf 0.31 0.38
SESE 5 0.8 0.043 Inf 0.72 0.89
SESE 10 0.67 0.043 Inf 0.59 0.75

3.2.2 Height at year 10

Sprout heights at year 10 were modeled with a normal response and a log link. The best model included species and treatment, but no interactions in the fixed effects. This suggests that treatments do not affect species differentially in terms of the mean response (height at year 10). It also included a model for dispersion (log link) with predictors species, treatment, and their interaction (Listing 3.4).

Listing 3.4 
Family: gaussian (log) 
Conditional: ht ~ treat + spp + (0 + spp | plot)  
Dispersion: ~spp * treat (log)

Because the best model did not contain a species x treatment interaction for the mean response, treatment comparisons were parallel between species. The GS treatment resulted in greater heights in year 10 than the other treatments (0.001 < p < 0.05). Predicted mean height for redwood ranged from 10.64 m in the GS treatment to 6.3 m in the HD treatment. For tanoak, predicted mean height ranged from 5.2 m in the GS treatment to 3.08 m in the HD treatment. Predicted mean heights followed the pattern GS > LD > HA ≥ HD (Figure 3.6).

Figure 3.6: Predicted mean height and 95% confidence intervals (gray bars) for redwood and tanoak stump sprouts 10 years after harvest using four different harvest treatments. Non-overlapping blue arrows indicate statistically significant differences between treatments within a species.
Table 3.7: Height (m) of measured redwood and tanaok sprouts 10 years after harvest treatments with four different over-story densities. The asymptotic 95% confidence intervals are based on the normal approximation.
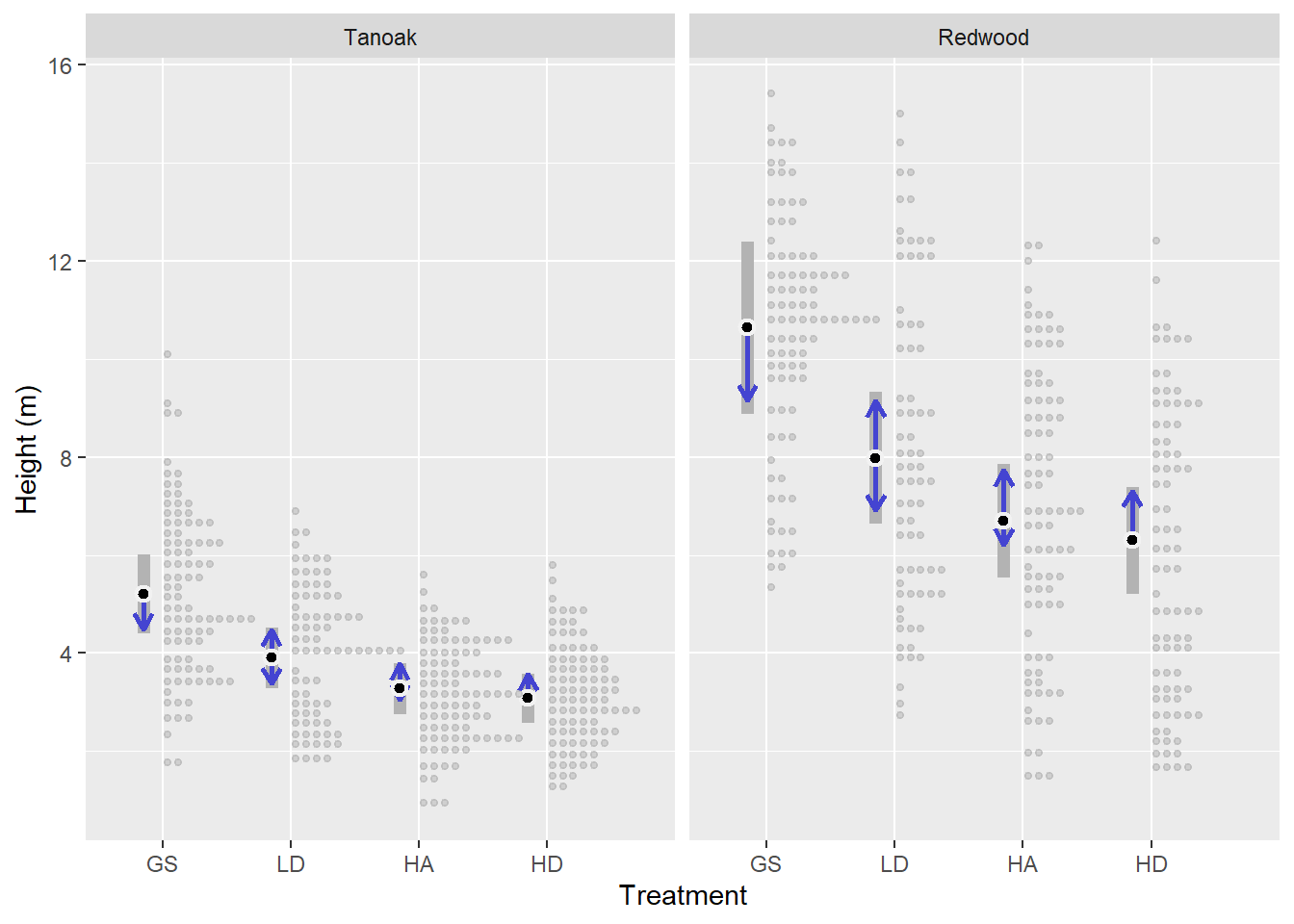
spp year estimate SE df asymp.LCL asymp.UCL
LIDE GS 5.2 0.41 Inf 4.4 6
LIDE LD 3.9 0.31 Inf 3.3 4.5
LIDE HA 3.3 0.27 Inf 2.8 3.8
LIDE HD 3.1 0.25 Inf 2.6 3.6
SESE GS 10.6 0.9 Inf 8.9 12.4
SESE LD 8 0.69 Inf 6.6 9.3
SESE HA 6.7 0.59 Inf 5.5 7.8
SESE HD 6.3 0.55 Inf 5.2 7.4
Table 3.8: Pairwise comparisons of treatments within species for height (m) of measured redwood and tanoak sprouts 10 years after harvest. The P-values are based on the normal approximation.
spp contrast estimate SE df p.value
LIDE GS - LD 1.3 0.5 Inf 0.05
LIDE GS - HA 1.93 0.48 Inf 0
LIDE GS - HD 2.12 0.47 Inf 0
LIDE LD - HA 0.63 0.4 Inf 0.4
LIDE LD - HD 0.82 0.39 Inf 0.16
LIDE HA - HD 0.19 0.36 Inf 0.95
SESE GS - LD 2.66 1.03 Inf 0.05
SESE GS - HA 3.94 0.98 Inf 0
SESE GS - HD 4.33 0.97 Inf 0
SESE LD - HA 1.29 0.82 Inf 0.4
SESE LD - HD 1.68 0.81 Inf 0.16
SESE HA - HD 0.39 0.75 Inf 0.95

3.3 Fuels

3.3.1 Pre-pct

Gamma distributed, linear multi-level models, with a log link were used for all six fuel class responses. Random intercepts were specified for three levels of nesting, representing sites, treatment blocks, and transect corners. All models except for the duff & litter model included a hurdle model to account for zeros, which was modeled with a logit link. For the 10-hr fuel model, the hurdle portion was modeled as a function of treatment, and for the others, it was modeled as a single rate for all observations. The 10-hr fuel model also included a dispersion model, which was modeled with a log link, using treatment as a predictor (Table 3.9).

Table 3.9: Model specifications for six fuel classes before pct.
class Family Link Conditional Dispersion (log) Hurdle (logit)
Duff & Litter Gamma log load ~ trt + (1 | site) + (1 | block) + (1 | corner) ~1 ~0
1-hr Gamma log load ~ trt + (1 | site) + (1 | block) + (1 | corner) ~1 ~1
10-hr Gamma log load ~ trt + (1 | site) + (1 | block) + (1 | corner) ~trt ~trt
100-hr Gamma log load ~ trt + (1 | site) + (1 | block) + (1 | corner) ~1 ~1
1,000-hr Gamma log load ~ trt + (1 | site) + (1 | block) + (1 | corner) ~1 ~1
Vegetation Gamma log load ~ trt + (1 | site) + (1 | block) + (1 | corner) ~1 ~1

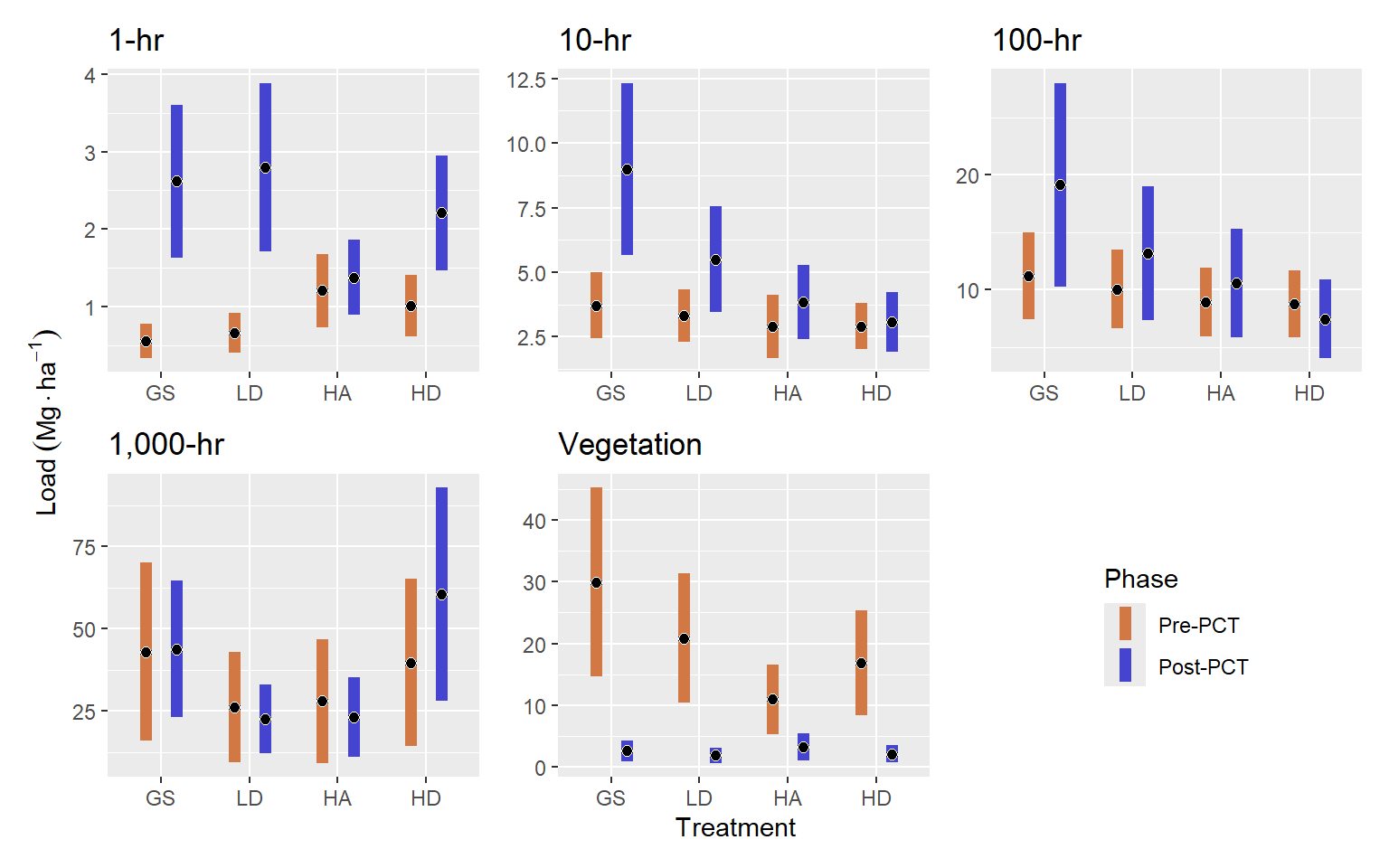
For Duff & Litter, the largest difference was between the HD and HA treatments. The HD treatment had about 54.4 Mg ha-1, and was about 14.39 Mg ha-1 greater than the HA treatment (p = 0.09). Generally, all treatments were similar, with estimated loading of around 47 Mg ha-1.

One-hour fuels were highest in the HA treatment, with an expected value of 1.2 Mg ha-1, which was about Mg ha-1 greater than in the GS treatment (p = 0.03). One-hour fuels in the LD and HD treatments were intermediate but the LD was more similar to the GS and the HD was more similar to the HA treatment.

Ten, hundred and thousand-hour fuels were statistically, very similar across treatments (p ≥ 0.7). Treatment averages had maximum differences of around 1, 3, and 10 Mg ha-1 for ten, hundred, and thousand-hour fuels, respectively.

Vegetative fuel loading was greatest in the GS treatment, with an expected value of 29.94 Mg ha-1, which was about
18.95 Mg ha-1 greater than in the HA treatment (p = 0.05) and LD and HD treatments were intermediate. (Figure 3.7).

Figure 3.7: Estimated marginal means (black dots) confidence intervals (gray bands) and comparisons (blue arrows) of fuel loading across four treatments for six different fuel-class models. Non-overlapping blue arrows indicates statistical significance at the α = 0.05 level.
Table 3.10: Estimated marginal means (Mg ha-1) for six fuel classes and four overstory treatments 10 years after partial harvest and prior to pre-commercial thinning (PCT). The asymptotic 95% confidence intervals are based on the normal approximation.
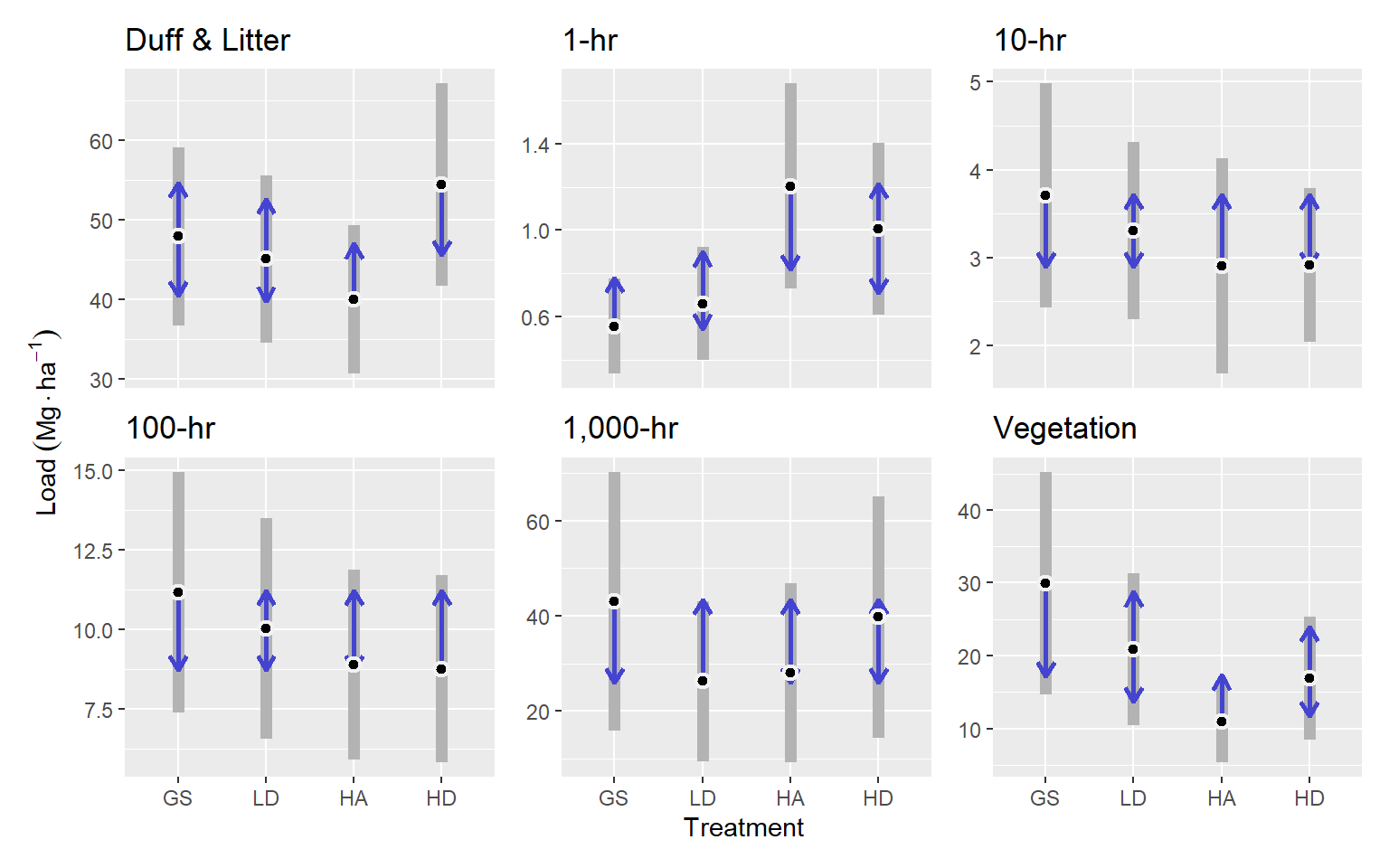
class treatment estimate SE df asymp.LCL asymp.UCL
dufflitter gs 47.93 5.69 Inf 36.76 59.09
dufflitter ld 45.09 5.35 Inf 34.6 55.59
dufflitter ha 40.01 4.75 Inf 30.71 49.32
dufflitter hd 54.4 6.46 Inf 41.74 67.06
onehr gs 0.55 0.11 Inf 0.33 0.77
onehr ld 0.66 0.13 Inf 0.4 0.92
onehr ha 1.2 0.24 Inf 0.73 1.68
onehr hd 1.01 0.2 Inf 0.61 1.41
tenhr gs 3.71 0.65 Inf 2.43 4.98
tenhr ld 3.31 0.52 Inf 2.3 4.32
tenhr ha 2.9 0.63 Inf 1.68 4.13
tenhr hd 2.91 0.45 Inf 2.04 3.79
hundhr gs 11.17 1.92 Inf 7.41 14.93
hundhr ld 10.03 1.76 Inf 6.58 13.47
hundhr ha 8.9 1.52 Inf 5.92 11.88
hundhr hd 8.76 1.49 Inf 5.84 11.69
thoushr gs 43.08 13.84 Inf 15.95 70.22
thoushr ld 26.25 8.58 Inf 9.43 43.06
thoushr ha 28.06 9.58 Inf 9.29 46.83
thoushr hd 39.75 12.94 Inf 14.38 65.11
veg gs 29.94 7.78 Inf 14.69 45.19
veg ld 20.88 5.32 Inf 10.45 31.3
veg ha 10.99 2.86 Inf 5.39 16.6
veg hd 16.86 4.32 Inf 8.4 25.32
Table 3.11: Pairwise comparisons of treatments for six fuel classes before pct. P-values were adjusted for multiple comparisons using the Tukey method and are based on normal approximations.
class contrast estimate SE df p.value
onehr gs - ha -0.6491 0.24 Inf 0.033
veg gs - ha 18.947 7.46 Inf 0.054
dufflitter ha - hd -14.3869 6.16 Inf 0.09
onehr ld - ha -0.5439 0.24 Inf 0.115
onehr gs - hd -0.4529 0.2 Inf 0.119
veg ld - ha 9.8847 5.29 Inf 0.242
veg gs - hd 13.0772 7.78 Inf 0.334
onehr ld - hd -0.3477 0.21 Inf 0.353
dufflitter ld - hd -9.3078 6.38 Inf 0.463
dufflitter gs - ha 7.9119 5.63 Inf 0.497
veg ha - hd -5.8698 4.47 Inf 0.555
hundhr gs - hd 2.405 2.13 Inf 0.671
veg gs - ld 9.0623 8.11 Inf 0.679
thoushr gs - ld 16.832 15.77 Inf 0.71
hundhr gs - ha 2.2729 2.15 Inf 0.715
tenhr gs - hd 0.7915 0.79 Inf 0.748
dufflitter gs - hd -6.475 6.53 Inf 0.755
dufflitter ld - ha 5.0791 5.43 Inf 0.786
thoushr gs - ha 15.0192 16.34 Inf 0.795
thoushr ld - hd -13.4991 14.91 Inf 0.802
tenhr gs - ha 0.8008 0.9 Inf 0.809
thoushr ha - hd -11.6863 15.4 Inf 0.873
onehr ha - hd 0.1962 0.27 Inf 0.889
onehr gs - ld -0.1051 0.15 Inf 0.896
veg ld - hd 4.015 5.85 Inf 0.902
hundhr ld - hd 1.2626 2.02 Inf 0.924
tenhr ld - hd 0.3916 0.68 Inf 0.94
hundhr ld - ha 1.1306 2.03 Inf 0.945
hundhr gs - ld 1.1424 2.28 Inf 0.959
tenhr ld - ha 0.401 0.81 Inf 0.96
tenhr gs - ld 0.3998 0.83 Inf 0.963
dufflitter gs - ld 2.8328 5.93 Inf 0.964
thoushr gs - hd 3.3329 18.36 Inf 0.998
thoushr ld - ha -1.8127 12.21 Inf 0.999
hundhr ha - hd 0.132 1.85 Inf 1
tenhr ha - hd -0.0094 0.77 Inf 1
Table 3.12: Modeled grand means Mg ha-1 of fuel loading 10 years after harvest and prior to PCT. The asymptotic 95% confidence intervals are based on the normal approximation.
class 1 estimate SE df asymp.LCL asymp.UCL
dufflitter overall 46.86 4.21 Inf 38.6 55.1
onehr overall 0.86 0.12 Inf 0.63 1.1
tenhr overall 3.21 0.28 Inf 2.65 3.8
hundhr overall 9.71 1.1 Inf 7.56 11.9
thoushr overall 34.29 6.31 Inf 21.93 46.6
veg overall 19.67 3.52 Inf 12.77 26.6

3.3.2 Post-pct

After PCT, the response for all six fuel classes were modeled with a gamma distribution and a log link, and included the same multi-level random effects as for the pre-pct models. Dispersion models with treatment as the only predictor were included for 1-hr and 100-hr fuel classes. All models included a hurdle portion to model zeros using a logit link. For 100-hr fuels, the hurdle portion included treatment and site as predictors. For the rest, a constant rate of zeros for all observations was used (Table 3.13).

Table 3.13: Model specifications for six fuel classes after pct.
class Family Link Conditional Dispersion (log) Hurdle (logit)
1-hr Gamma log load ~ trt + (1 | site) + (1 | block) + (1 | corner) ~trt + site ~1
10-hr Gamma log load ~ trt + (1 | site) + (1 | block) + (1 | corner) ~1 ~1
100-hr Gamma log load ~ trt + (1 | site) + (1 | block) + (1 | corner) ~trt + site ~trt + site
1,000-hr Gamma log load ~ trt + (1 | site) + (1 | block) + (1 | corner) ~1 ~1
Vegetation Gamma log load ~ trt + (1 | site) + (1 | block) + (1 | corner) ~1 ~1
Vegetation Difference Gamma log load ~ trt + (1 | site) + (1 | block) + (1 | corner) ~1 ~1

Unlike pre-pct fuel loading which differed little among treatments in terms of fine dead surface fuels, the PCT treatment resulted in additional fine dead surface fuels that differed significantly among treatments. Whereas vegetation fuel loading was reduced and differences between treatments were lessened. Unlike pre-commercial thinning resulted in greater stratification of treatments (Figure 3.8). One-hour fuels for most treatments were around 2.5 Mg ha-1, but the HA treatment was lower than these at about 1.38 Mg ha-1 (p <= ).

The GS treatment had the greatest 10-hr fuel loading with 9 Mg ha-1, which was greater than the LD, HA, and HD treatments by
3.5, 5.15, and 5.94 Mg ha-1, respectively ( p = 0.06, p < 0.001, and p = 0). The LD treatment also had about 2.43 Mg ha-1 more 10-hr fuels that the HD treatment (p = 0.03).

Hundred-hour fuels followed a similar trend as the 10-hr fuels. They were greatest in the GS treatment, with an average of about 19.12 Mg ha-1, which was about 11.69 Mg ha-1 greater than the HD treatment (p = 0.03).

Thousand-hour fuels were greatest in the HD treatment, with an average of about r fuel_post_means$thoushr$hd$estimate Mg ha-1, which was about 37.71 Mg ha-1 greater than the LD and HA treatments (p <= 0.14). The GS treatment was intermediate.

Fuel loading for live vegetation was similar across treatments at around 2.3 Mg ha-1.

The difference in vegetation loading before and after PCT was greatest in the GS treatment at about 29.6 Mg ha-1, which was greater than the HA and HD treatments by about 18 Mg ha-1 (p = 0.09 and p = 0.05, respectively). The LD treatment was intermediate.

Figure 3.8: Estimated marginal means (black dots) confidence intervals (gray bars) and statistical comparisons (blue arrows) of fuel loading across four treatments for six different fuel-class models. Non-overlapping blue arrows indicates statistical significance at the α = 0.05 level. Vegetation difference equals the transect level difference in vegetation load in the pre and post-pct conditions. This represents slash fuels recruited to the forest floor following the pre-commercial thinning.
Table 3.14: Estimated marginal means (Mg ha-1) for six fuel classes and four overstory treatments 10 years after partial harvest and after pre-commercial thinning (PCT). The asymptotic 95% confidence intervals are based on the normal approximation.
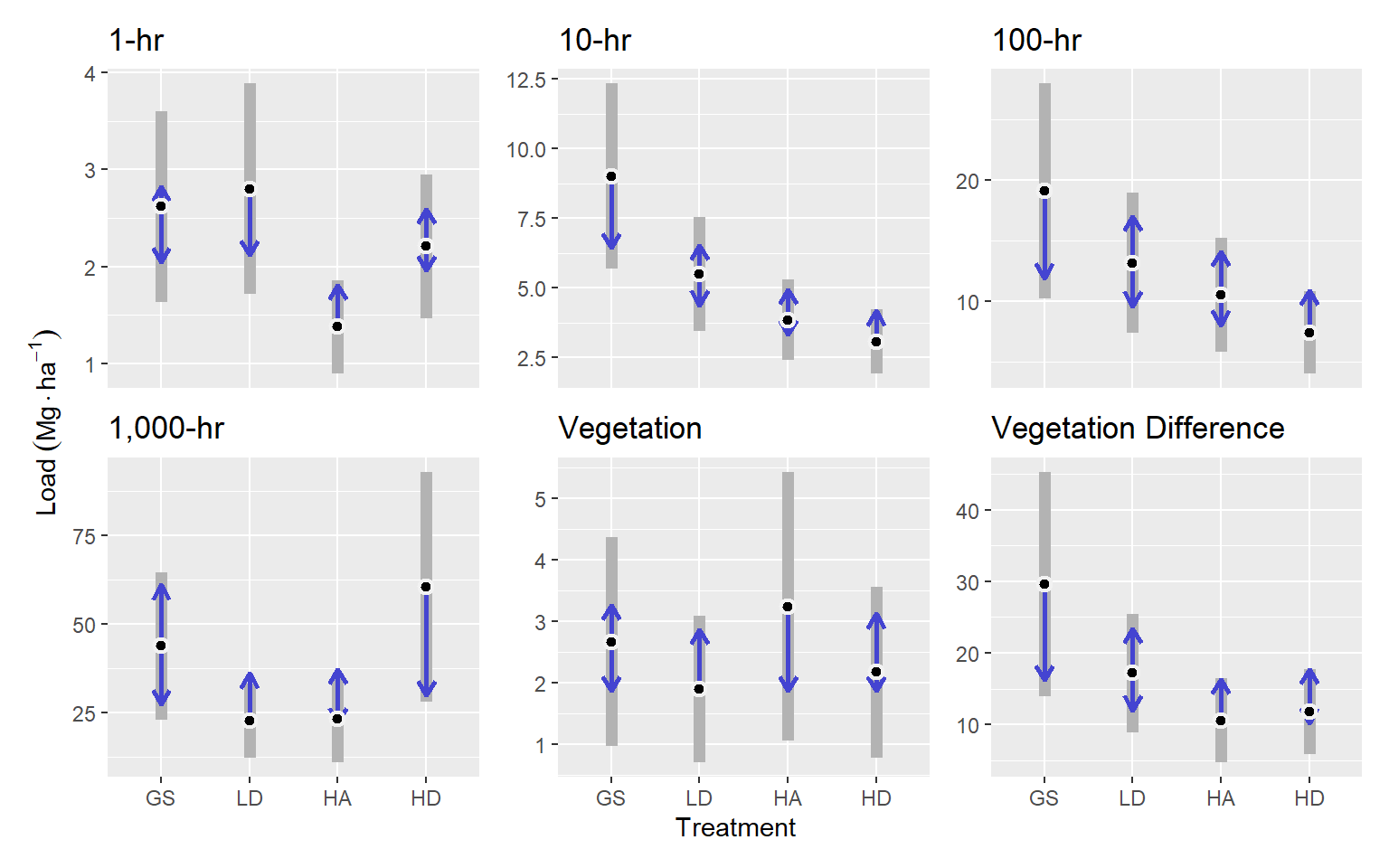
class treatment estimate SE df asymp.LCL asymp.UCL
onehr gs 2.6 0.5 Inf 1.63 3.6
onehr ld 2.8 0.55 Inf 1.71 3.9
onehr ha 1.4 0.25 Inf 0.89 1.9
onehr hd 2.2 0.38 Inf 1.47 2.9
tenhr gs 9 1.7 Inf 5.68 12.3
tenhr ld 5.5 1.05 Inf 3.44 7.6
tenhr ha 3.9 0.73 Inf 2.41 5.3
tenhr hd 3.1 0.59 Inf 1.92 4.2
hundhr gs 19.1 4.52 Inf 10.26 28
hundhr ld 13.2 2.97 Inf 7.36 19
hundhr ha 10.5 2.41 Inf 5.81 15.3
hundhr hd 7.4 1.74 Inf 4.03 10.8
thoushr gs 43.9 10.61 Inf 23.08 64.7
thoushr ld 22.8 5.33 Inf 12.31 33.2
thoushr ha 23.2 6.21 Inf 11.04 35.4
thoushr hd 60.5 16.55 Inf 28.05 92.9
veg gs 2.7 0.87 Inf 0.96 4.4
veg ld 1.9 0.61 Inf 0.7 3.1
veg ha 3.2 1.12 Inf 1.06 5.4
veg hd 2.2 0.71 Inf 0.78 3.6
veg_diff gs 29.6 7.99 Inf 13.95 45.3
veg_diff ld 17.2 4.22 Inf 8.89 25.4
veg_diff ha 10.6 2.98 Inf 4.74 16.4
veg_diff hd 11.8 3.02 Inf 5.91 17.7
Table 3.15: Pairwise comparisons of treatments for six fuel classes after pct. P-values were adjusted for multiple comparisons using the Tukey method and are based on normal approximations.
class contrast estimate SE df p.value
tenhr gs - hd 5.94 1.46 Inf 0.00026
tenhr gs - ha 5.15 1.43 Inf 0.00172
onehr ld - ha 1.42 0.43 Inf 0.00585
onehr gs - ha 1.24 0.39 Inf 0.00889
onehr ha - hd -0.83 0.26 Inf 0.00919
hundhr gs - hd 11.69 4.16 Inf 0.02573
tenhr ld - hd 2.43 0.87 Inf 0.02637
veg_diff gs - ha 19.03 7.48 Inf 0.05357
tenhr gs - ld 3.5 1.41 Inf 0.06286
veg_diff gs - hd 17.78 7.55 Inf 0.08602
thoushr ld - hd -37.71 17.15 Inf 0.12359
thoushr ha - hd -37.27 17.43 Inf 0.14104
hundhr ld - hd 5.75 2.75 Inf 0.1565
hundhr gs - ha 8.59 4.21 Inf 0.17315
tenhr ld - ha 1.65 0.88 Inf 0.24322
thoushr gs - ld 21.12 11.6 Inf 0.26381
thoushr gs - ha 20.67 12.01 Inf 0.31242
veg_diff gs - ld 12.44 7.67 Inf 0.36644
veg_diff ld - ha 6.59 4.3 Inf 0.41898
onehr ld - hd 0.59 0.42 Inf 0.49237
hundhr gs - ld 5.95 4.31 Inf 0.51297
veg ld - ha -1.35 0.98 Inf 0.51617
hundhr ha - hd 3.1 2.32 Inf 0.54089
veg_diff ld - hd 5.35 4.3 Inf 0.59869
tenhr ha - hd 0.79 0.64 Inf 0.60281
veg ha - hd 1.07 0.97 Inf 0.68792
onehr gs - hd 0.41 0.37 Inf 0.6903
veg gs - ld 0.77 0.76 Inf 0.7434
hundhr ld - ha 2.65 2.91 Inf 0.80002
thoushr gs - hd -16.6 19.3 Inf 0.82556
veg gs - hd 0.49 0.8 Inf 0.92729
veg gs - ha -0.58 1.04 Inf 0.94512
veg ld - hd -0.28 0.66 Inf 0.97521
onehr gs - ld -0.18 0.48 Inf 0.98118
veg_diff ha - hd -1.24 3.52 Inf 0.98495
thoushr ld - ha -0.45 7.78 Inf 0.99993
Table 3.16: Modeled grand means Mg ha-1 of fuel loading 10 years after harvest and PCT. The asymptotic 95% confidence intervals are based on the normal approximation.
class 1 estimate SE df asymp.LCL asymp.UCL
onehr overall 2.3 0.36 Inf 1.5 3
tenhr overall 5.4 0.84 Inf 3.7 7
hundhr overall 12.6 2.2 Inf 8.3 16.9
thoushr overall 37.6 5.61 Inf 26.6 48.6
veg overall 2.5 0.65 Inf 1.2 3.8
veg_diff overall 17.3 3.33 Inf 10.8 23.8

3.3.3 Pre-post commercial thinning comparison

The PCT of 10-year-old vegetation dramatically reduced live surface fuels, predictably leading to varying increases in loading across 1- 10- and 100-hr fuels. Specifically PCT led to a small increase in average 100-hr fuel loading, only for the GS treatment, increased 10-hr fuels in the GS and LD treatments, and increased 1-hr fuels for all but the HA treatment (Figure 3.9). However these results were not statistically comparable, due to slightly different model structures.

Figure 3.9: Estimated marginal means (black dots) and confidence intervals (colored bars) of fuel loading across four treatments and five different fuel classes, before and after PCT. Pre- and Post PCT models within a treatment are from similar, but not necessarily identical models.