11 Reneration data summary

Code

library(marginaleffects)
library(tidyr)
library(ggdist)
library(patchwork)
library(vegan)
library(glmmTMB)
library(DHARMa)
library(ggplot2)
library(dplyr)

load("regen_wrangled.rda")

Some functions and constants that I need later on, these might should get moved to their own function and sourced.

Code

# The metric foresters constant: diameter in cm to area of a circle in square
# meters
for_const <- function(dbh) {
  pi * dbh^2 / (4 * 10000)
}

# I need a mapping so that each species gets a unique color, I'll make this a
# function that takes a palette function from the scales package and returns a
# named vector

spp_col <- function(data, .palfun, ...) {
  pal <- .palfun(...)
  spp <- unique(data$spp)
  purrr::set_names(pal(length(spp)), spp)
}

11.1 Objectives

Determine if there are significant differences in species composition, or size class distribution between treatments

This objective is somewhat vague because I am not familiar with the statistical techniques used for the weighted (diameter), multi-variate (species) distribution data that we have.

For starters, I will look at summaries of size class distributions by species. I will report densities in terms of trees per hectare (tph). Our plots were fixed area, 4-m-radius plots, or 50.27 m². Each stem in a veg. plot represents 198.94 stems/ha. As shown in Figure 1.2, there are:

64 veg. plots in the experiment
16 in a treatment
4 in a macro plot

This plot is a little difficult to interpret beccause of the large difference in counts from the smallest to largest stems. It might make more sense to look at regen smaller than 5 cm separately.

Code

# expansion factors at different aggregation levels
per_ha <- c(
  all = 1 / 64,
  treat = 1 / 16,
  plot = 1 / 4,
  corner = 1
) *
  (10000 / (16 * pi))

p <- regen |>
  ggplot(aes(dbh, fill = spp)) +
  stat_bin(aes(y = after_stat(count) * per_ha["treat"]), bins = 10) +
  facet_wrap(vars(treat), nrow = 1) +
  labs(y = expr(trees %.% ha^-1))
p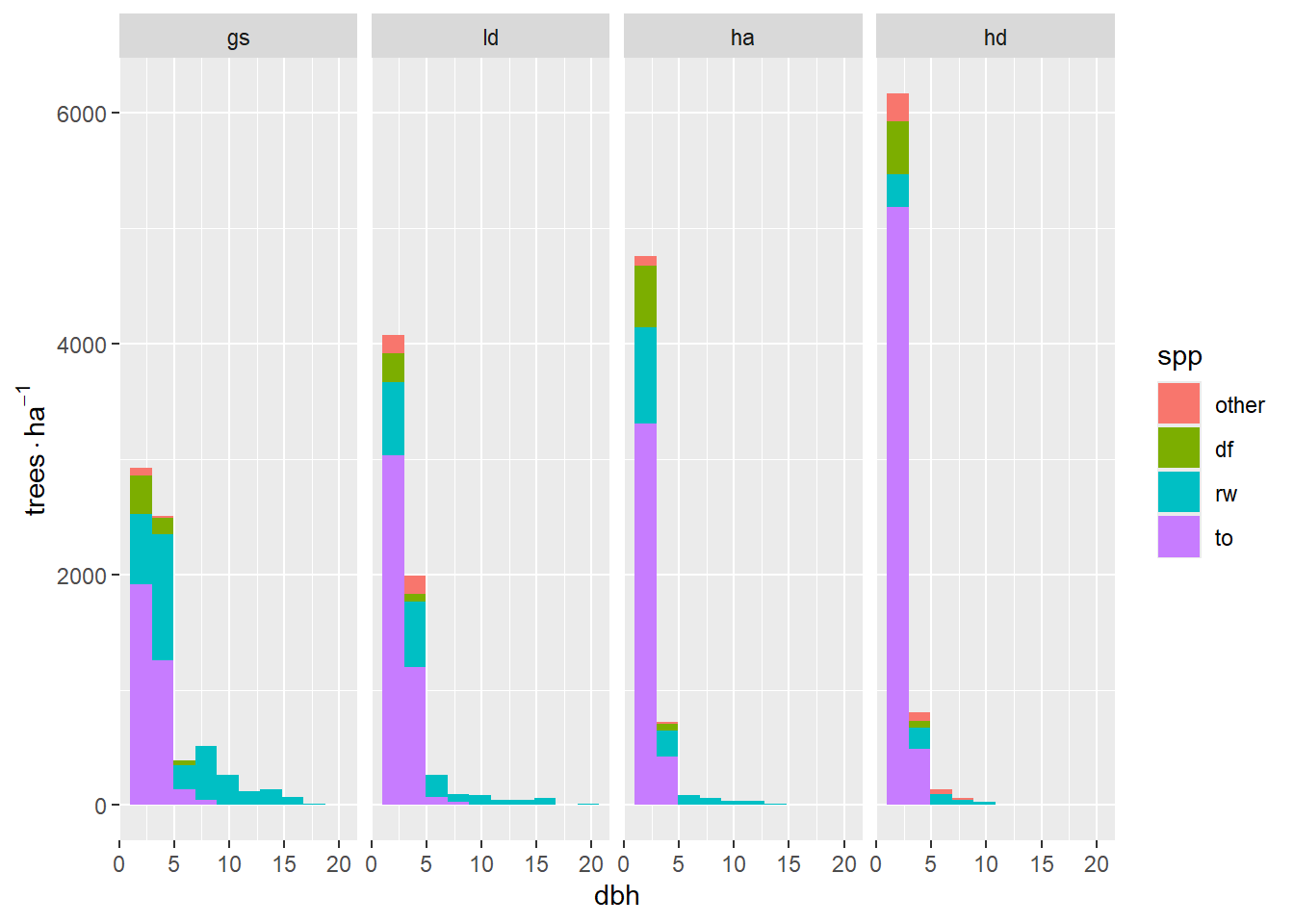

Figure 11.1: Histogram of regen by species and size class for each treatment.

Splitting the analysis at 5-cm-diameter stems shows a clear trend in treatments from most to least available light. Over this gradient, the number of 1.3-cm stems increases, and the 3.8-cm stems decrease, almost proportionally — and most of this is due to tanoak. For >= 5-cm stems, the effect is a fairly homogeneous decrease in the number of stems. There are few tanoak, Douglas-fir are only in the brightest areas. Mostly redwood (number of stems) shows a strong correlation with available light.

Code

raw_hist2 <- function(group, bin_breaks, scale_breaks, text_pos) {
  generate_facet_totals <- function(data) {
    dplyr::summarize(
      data,
      .by = treat,
      n = paste("Total: ", round(n() * per_ha["treat"])),
    )
  }
  colors <- spp_col(regen, scales::brewer_pal, palette = "Set2")
  regen |>
    filter({{ group }}) |>
    ggplot2::ggplot(aes(dbh, fill = forcats::fct_reorder(spp, spp, length))) +
    stat_bin(
      aes(y = after_stat(count) * per_ha["treat"]),
      breaks = bin_breaks
    ) +
    ggpp::geom_text_npc(
      data = generate_facet_totals,
      aes(npcx = "center", npcy = "top", label = n, fill = NULL)
    ) +
    facet_wrap(vars(treat), nrow = 1) +
    labs(y = expression(trees %.% ha^-1), x = "dbh (cm)", fill = "spp") +
    scale_x_continuous(breaks = scale_breaks) +
    scale_y_continuous(expand = expansion(c(0.05, 0.2))) +
    scale_fill_manual(values = colors) +
    theme_bw()
}

raw_hist2(dbh < 5, seq(0, 17.5, 2.5), seq(0, 15, 5), c(2.5, 6000)) /
  raw_hist2(dbh >= 5, seq(0, 17.5, 2.5), seq(0, 15, 5), c(27, 600))

Registered S3 methods overwritten by 'ggpp':
  method                  from   
  heightDetails.titleGrob ggplot2
  widthDetails.titleGrob  ggplot2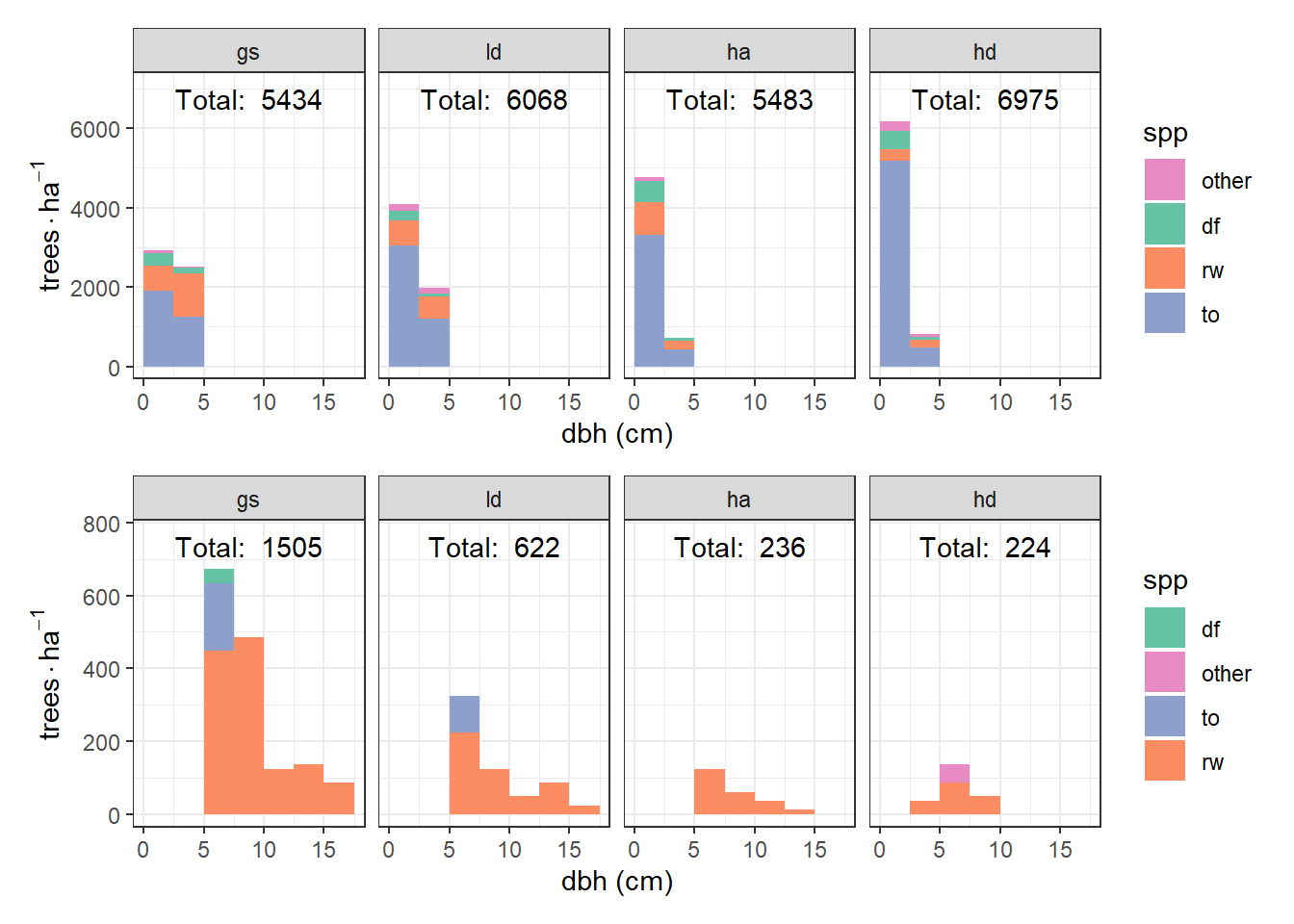

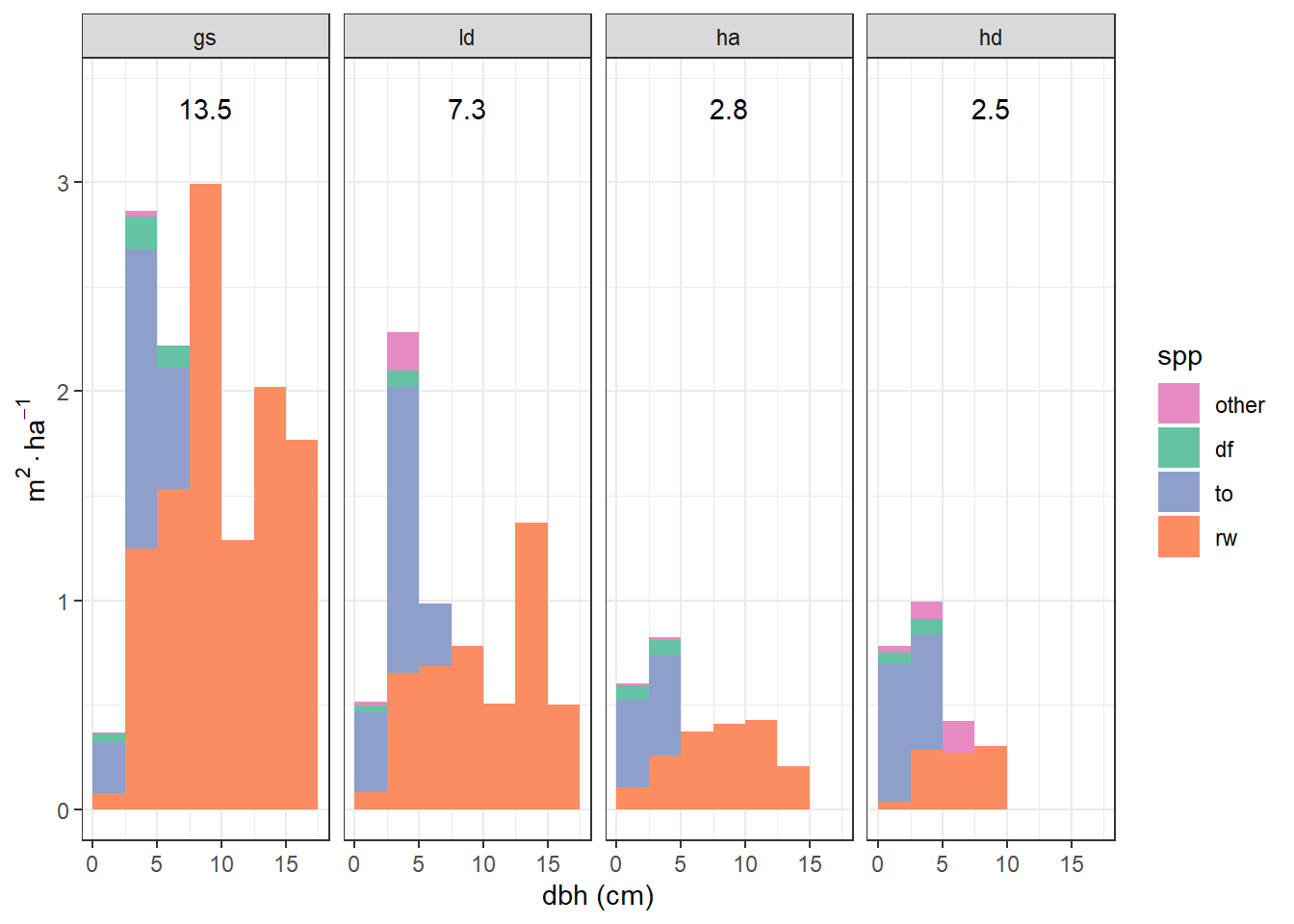
Figure 11.2: Histograms of regen by species and size class. On top are stems less than five centimeters in diameter, and stems greater than five centimeters are on the bottom.

This is interesting, but I wonder what this would look like in terms of basal area, which is more biologically relevant than number of stems.

Code

local({
  bin_breaks <- seq(0, 17.5, 2.5)
  scale_breaks <- seq(0, 15, 5)
  facet_total_label <- function(data) {
    summarize(
      data,
      .by = treat,
      ba_ha = round(sum(per_ha["treat"] * for_const(dbh)), 1)
    )
  }
  regen |>
    ggplot(aes(
      dbh,
      fill = forcats::fct_reorder(spp, dbh, .fun = ~ sum(.x^2))
    )) +
    stat_bin(
      aes(weight = per_ha["treat"] * for_const(dbh)),
      breaks = bin_breaks
    ) +
    ggpp::geom_text_npc(
      data = facet_total_label,
      mapping = aes(npcx = "center", npcy = "top", label = ba_ha, fill = NULL)
    ) +
    facet_wrap(vars(treat), nrow = 1) +
    labs(y = expr(m^2 %.% ha^-1), x = "dbh (cm)", fill = "spp") +
    scale_y_continuous(expand = expansion(c(0.05, 0.2))) +
    scale_x_continuous(breaks = scale_breaks) +
    scale_fill_manual(
      values = spp_col(regen, scales::brewer_pal, palette = "Set2")
    ) +
    theme_bw()
})

12 Community analysis: Species and abundance (BA)

What I would like to know is, are there significant differences between treatments in terms of number of stems, or basal area each species and size class. For instance, a hypothetical result might be:

GS has 30% more redwood stems and 20% more redwood basal area than LD

The HD treatment resulted in more Douglas-fir than the LD and GS treatments

Above I visualize basal area by treatment, species, and size class. Here I’ll simplify and visualize just treatment and species.

Code

# I'm expanding my data to ensure that any plot missing a species observation is
# recorded as zeros.
colors <- spp_col(regen, scales::brewer_pal, palette = "Set2")

regen |>
  summarise(
    .by = c(site, treat, plot, spp),
    ba_ha = round(sum(per_ha["corner"] * for_const(dbh)), 2)
  ) |>
  complete(nesting(site, treat, plot), spp, fill = list(ba_ha = 0)) |>
  ggplot(aes(treat, ba_ha, fill = spp)) +
  geom_boxplot() +
  facet_wrap(~spp, scales = "free_y") +
  scale_fill_manual(values = colors)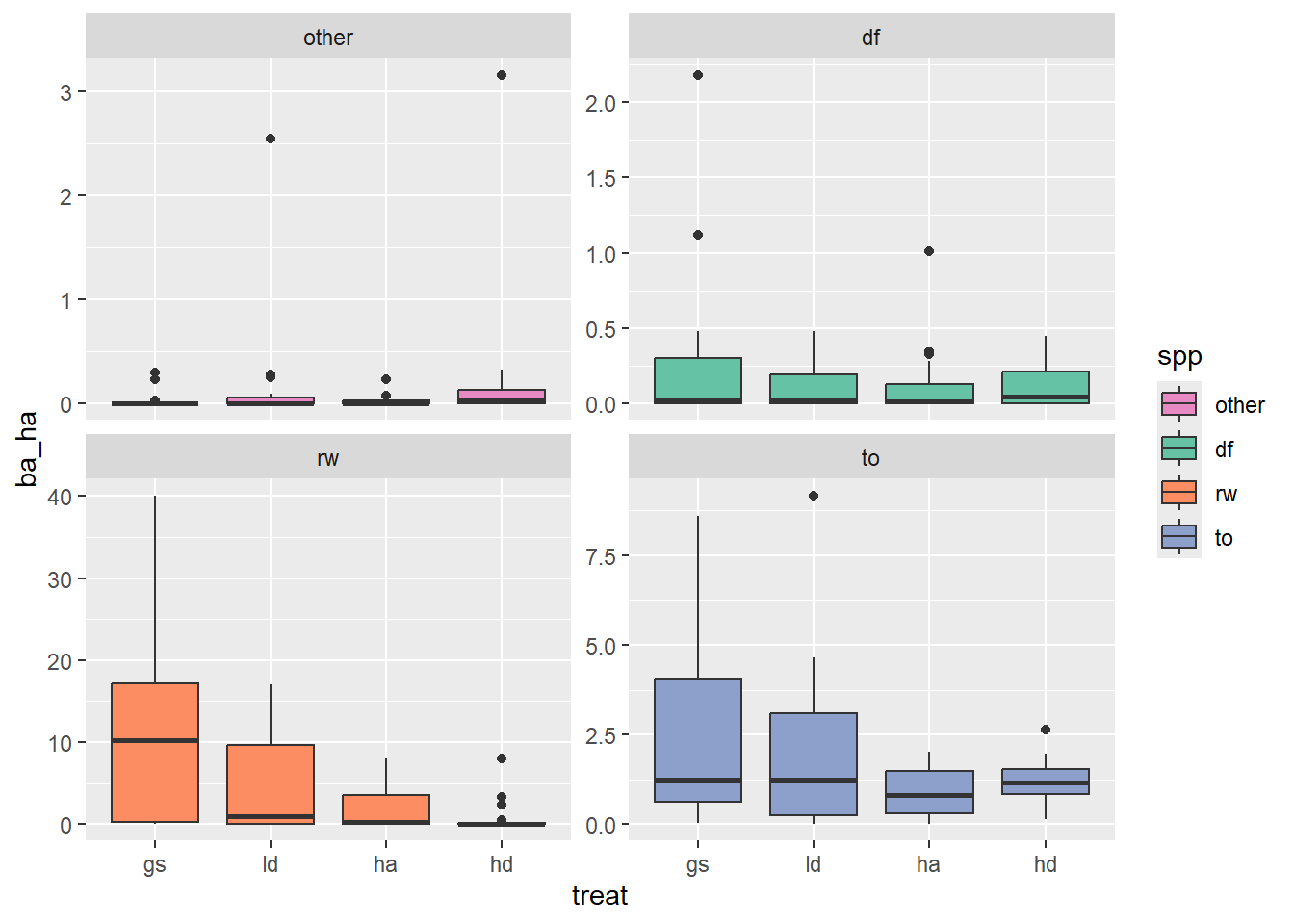

Here is another plot to get a better sense of what the data within treatment blocks looks like

Code

regen |>
  summarise(
    .by = c(site, treat, plot, spp),
    ba_ha = round(sum(per_ha["corner"] * for_const(dbh)), 2)
  ) |>
  complete(nesting(site, treat, plot), spp, fill = list(ba_ha = 0)) |>
  ggplot(aes(treat, ba_ha, fill = spp)) +
  geom_boxplot() +
  facet_wrap(~ spp + site, scales = "free_y") +
  scale_fill_manual(values = colors)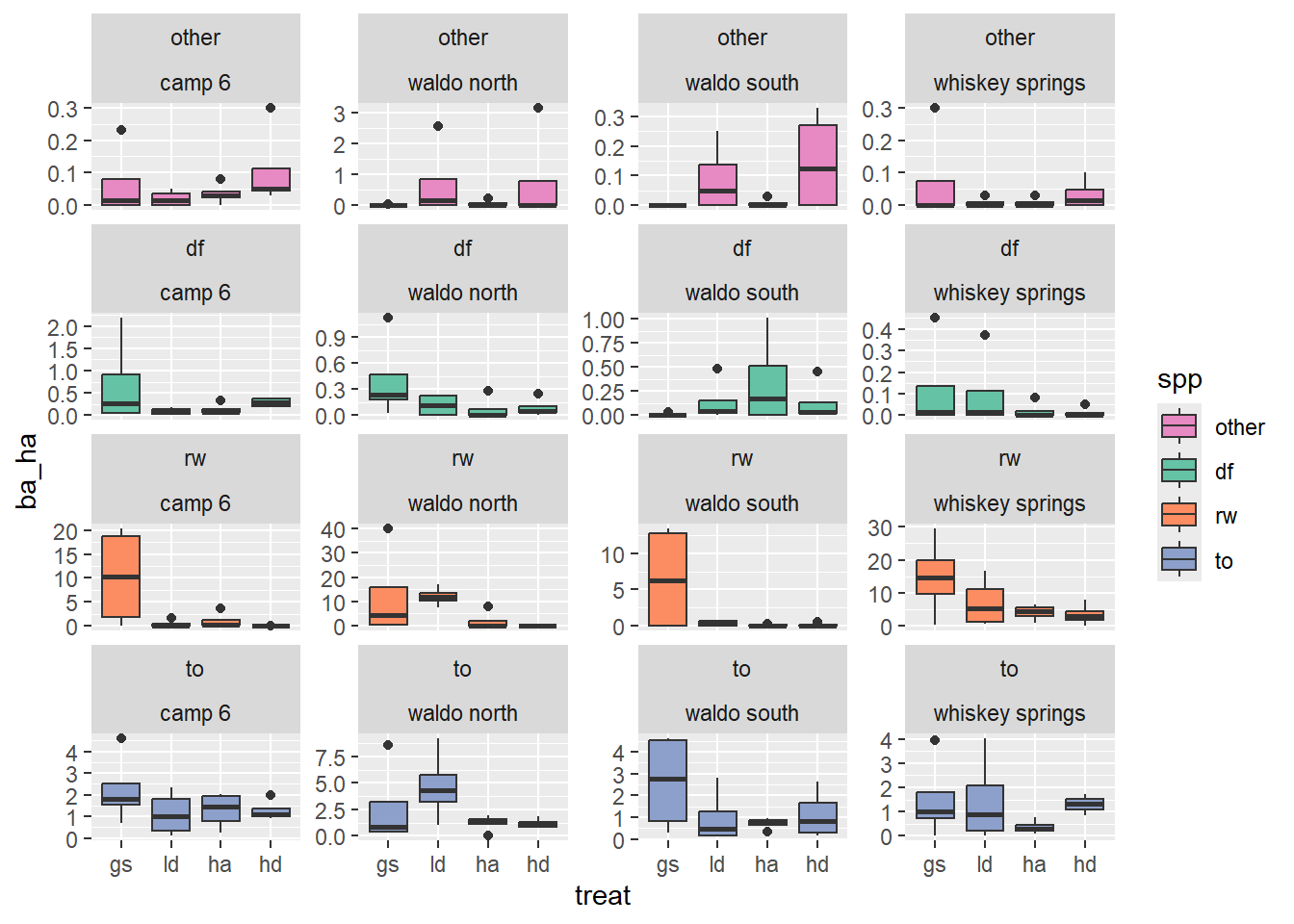

12.1 Permanova

While it’s not possible to include fully nested random effects using the adonis2 function, it seems important to try to include at least some accounting for grouping. I think site might be the most beneficial grouping level to capture because it captures differences in aspect, and also contains more observations than lower grouping levels.

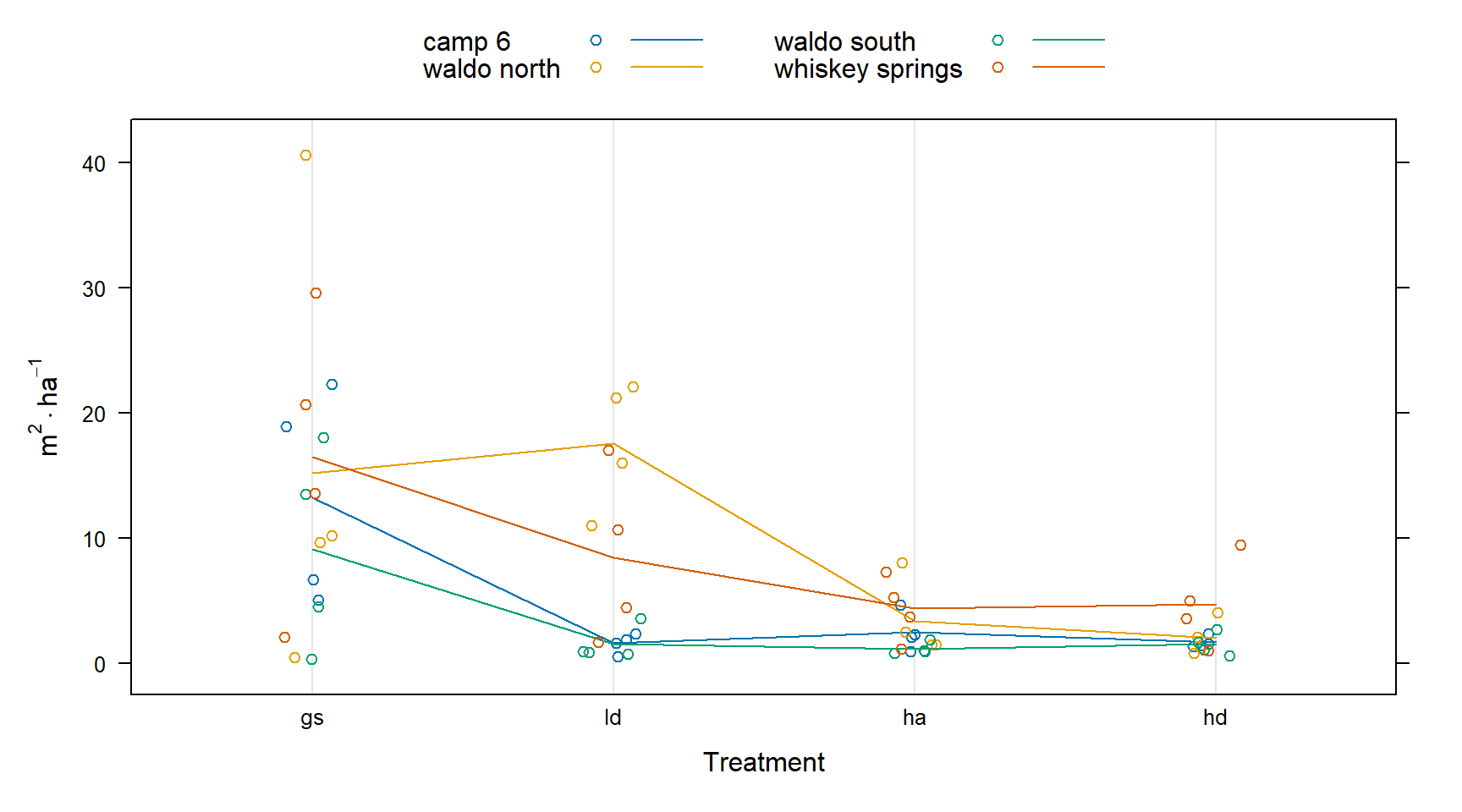
I will start out by visualizing the differences associated with sites.

This first plot shows that the whiskey spring site has generally higher basal area and that the waldo n site has an especially high basal area for the just the ld treatment.

Code

total_ba_ha <- regen |>
  summarize(
    .by = c(site, treat, plot),
    ba_ha = round(sum(per_ha["corner"] * for_const(dbh)), 2)
  )

dotplot(
  ba_ha ~ treat,
  total_ba_ha,
  groups = site,
  type = c("p", "a"),
  xlab = "Treatment",
  ylab = expression(m^2 %.% ha^-1),
  auto.key = list(columns = 2, lines = TRUE),
  jitter.x = TRUE
)

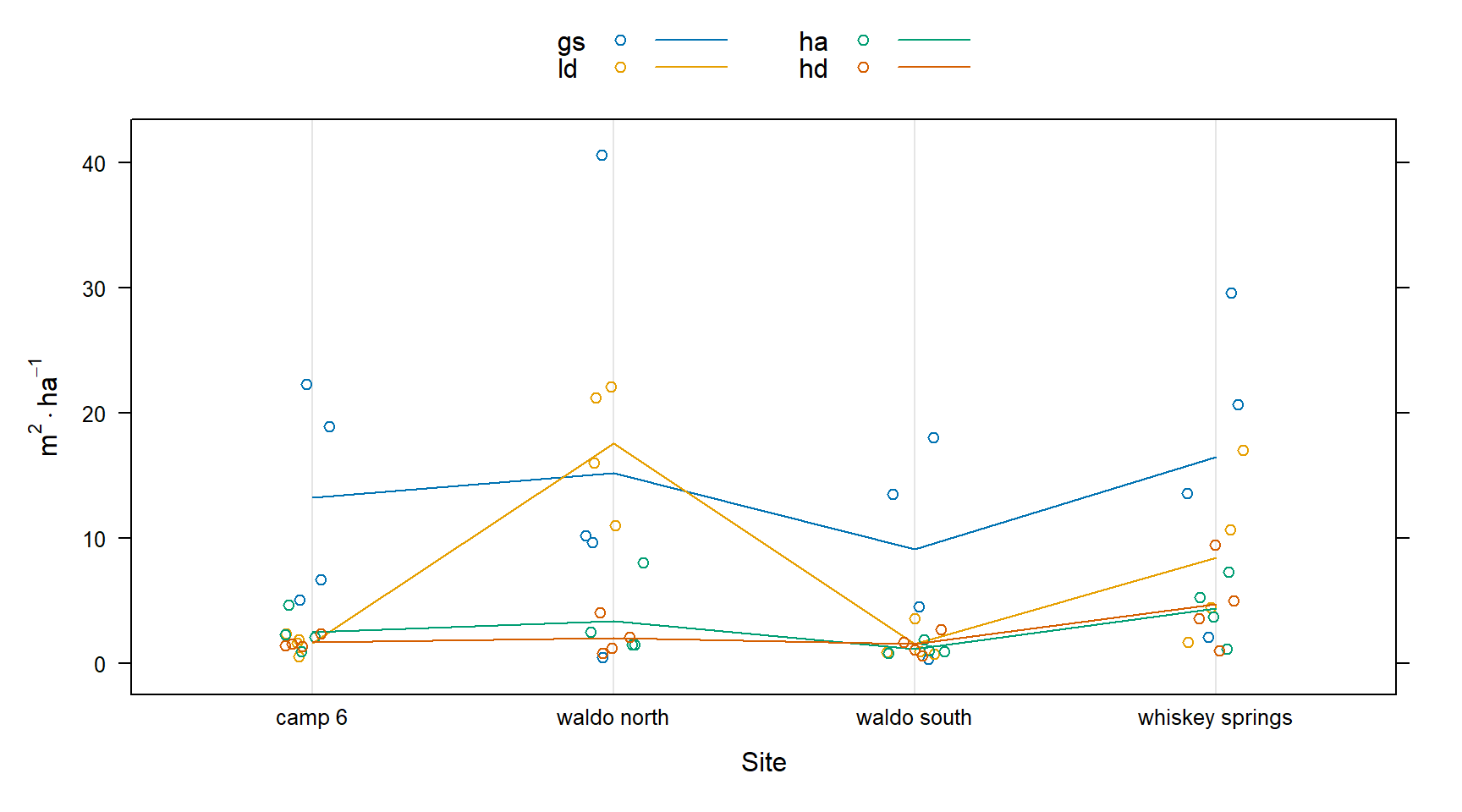
This figure shows that the site:treatment interaction is likely significant. There are similar trends across sites, but their magnitude is different depending on treatment.

Code

dotplot(
  ba_ha ~ site,
  total_ba_ha,
  groups = treat,
  type = c("p", "a"),
  xlab = "Site",
  ylab = expression(m^2 %.% ha^-1),
  auto.key = list(columns = 2, lines = TRUE),
  jitter.x = TRUE
)

Next, I’ll prepare the species data for analysis

Code

ba_ha <- regen |>
  summarise(
    .by = c(site, treat, plot, spp),
    ba_ha = round(sum(per_ha["corner"] * for_const(dbh)), 2)
  ) |>
  pivot_wider(names_from = spp, values_from = ba_ha) |>
  mutate(across(where(is.double), ~ replace_na(.x, 0)))

I took these from the help for adonis2, I’m not quite sure what aspect of the data they are showing yet.

Code

mod <- metaMDS(ba_ha[c("rw", "to", "df", "other")], trace = FALSE)
plot(mod)

ordiellipse(mod, ba_ha$site, kind = "ehull", label = TRUE)
ordispider(mod, ba_ha$site, lty = 3, col = "red")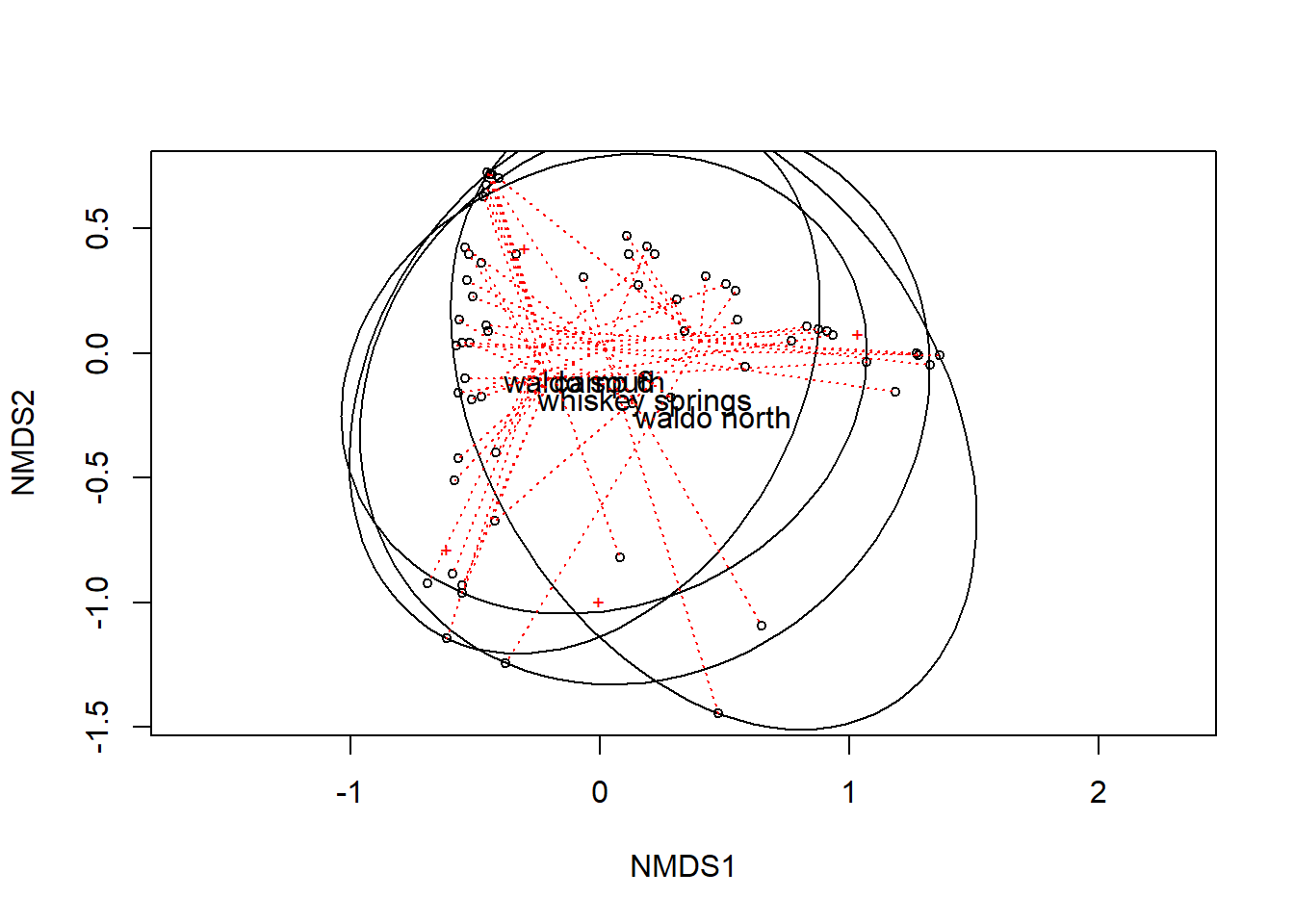

In the following models, the strata argument is used to: “Constrain perumtations within groups.” The first two models don’t include the site as strata.

When I include site as a fixed effect, p-values increase slightly.

Code

perms <- 500

adonis2(
  ba_ha[c("rw", "to", "df", "other")] ~ treat,
  data = ba_ha,
  permutations = perms
)

Permutation test for adonis under reduced model
Permutation: free
Number of permutations: 500

adonis2(formula = ba_ha[c("rw", "to", "df", "other")] ~ treat, data = ba_ha, permutations = perms)
         Df SumOfSqs      R2      F   Pr(>F)   
Model     3   2.1777 0.13288 3.0649 0.003992 **
Residual 60  14.2104 0.86712                   
Total    63  16.3881 1.00000                   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Code

adonis2(
  ba_ha[c("rw", "to", "df", "other")] ~ site + treat,
  data = ba_ha,
  permutations = perms
)

Permutation test for adonis under reduced model
Permutation: free
Number of permutations: 500

adonis2(formula = ba_ha[c("rw", "to", "df", "other")] ~ site + treat, data = ba_ha, permutations = perms)
         Df SumOfSqs      R2     F   Pr(>F)   
Model     6   4.2279 0.25799 3.303 0.001996 **
Residual 57  12.1602 0.74201                  
Total    63  16.3881 1.00000                  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

If I put site in strata, I get similar results.

Code

adonis2(
  ba_ha[c("rw", "to", "df", "other")] ~ treat,
  data = ba_ha,
  strata = ba_ha$site,
  permutations = perms
)

Permutation test for adonis under reduced model
Blocks:  strata 
Permutation: free
Number of permutations: 500

adonis2(formula = ba_ha[c("rw", "to", "df", "other")] ~ treat, data = ba_ha, permutations = perms, strata = ba_ha$site)
         Df SumOfSqs      R2      F   Pr(>F)   
Model     3   2.1777 0.13288 3.0649 0.001996 **
Residual 60  14.2104 0.86712                   
Total    63  16.3881 1.00000                   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

If I include the interaction of site:treatment as a fixed effect, it is not significant.

Code

with(
  ba_ha,
  adonis2(
    cbind(rw, to, df, other) ~ site + site:treat + treat,
    permutations = perms
  )
)

Permutation test for adonis under reduced model
Permutation: free
Number of permutations: 500

adonis2(formula = cbind(rw, to, df, other) ~ site + site:treat + treat, permutations = perms)
         Df SumOfSqs      R2      F   Pr(>F)   
Model    15   6.1261 0.37381 1.9103 0.003992 **
Residual 48  10.2620 0.62619                   
Total    63  16.3881 1.00000                   
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

I think we can safely conclude that ther are some significant differences in basal are composition (I assume at the alpha = 0.05 level) between treatments.

Next, we might consider where these differences (in abundance defined as basal area) are.

13 Species abundance model

We could ask about:

Differences between species within a treatment or
Differences between treatment within a species.

I will be focussing on the latter which is in keeping with the theme of the rest of my analysis. These differences have already been visualized above in Figure 12.1.

Again, I’m making zero observations explicit, effectively making our data presence-absence, rather than presence only.

Code

regen_pa <- regen |>
  summarize(
    .by = c(site, treat, plot, spp),
    ba_ha = round(sum(per_ha["corner"] * for_const(dbh)), 2)
  ) |>
  complete(nesting(site, treat, plot), spp, fill = list(ba_ha = 0))

regen_po <- regen |>
  summarize(
    .by = c(site, treat, plot, spp),
    ba_ha = round(sum(per_ha["corner"] * for_const(dbh)), 2)
  )

So, perhaps with our 16 observations per species/treatment, we can detect some differences in basal area with a multi-level model that accounts for non-independence of our sampling design.

Code

library(emmeans)

Welcome to emmeans.
Caution: You lose important information if you filter this package's results.
See '? untidy'

Code

m1 <- glmmTMB(ba_ha ~ treat * spp + (1 | site / treat / plot), regen_pa)
res1 <- simulateResiduals(m1)
plot(res1)

qu = 0.25, log(sigma) = -3.580392 : outer Newton did not converge fully.

qu = 0.25, log(sigma) = -3.926303 : outer Newton did not converge fully.

qu = 0.25, log(sigma) = -3.931632 : outer Newton did not converge fully.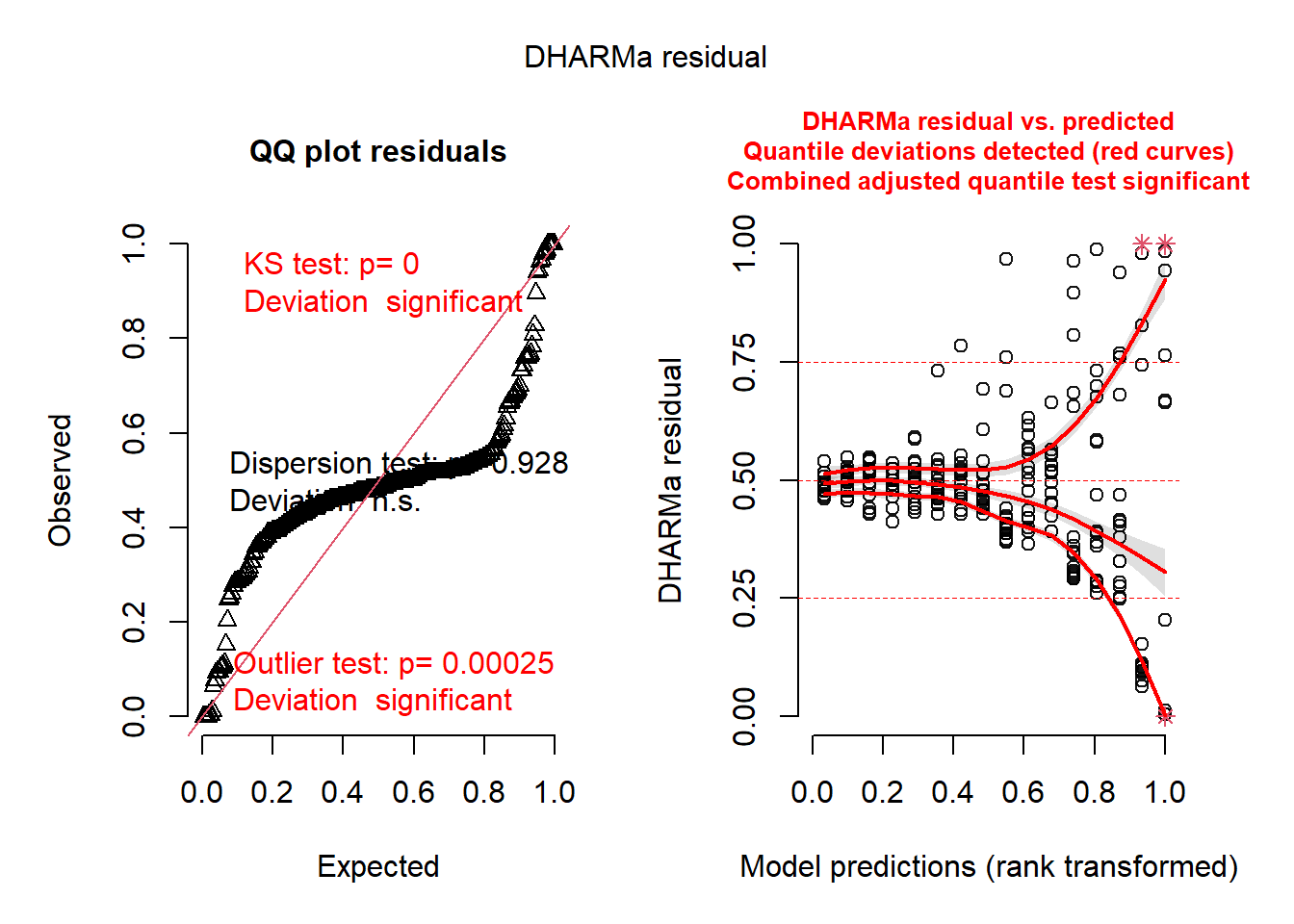

Code

m2 <- glmmTMB(
  ba_ha ~ treat * spp + (1 | site / treat),
  regen_pa,
  dispformula = ~spp
)
res2 <- simulateResiduals(m2)
plot(res2)

Code

m3 <- glmmTMB(
  ba_ha ~ treat * spp + (1 | site / treat),
  regen_pa,
  family = ziGamma(link = "log"),
  dispformula = ~spp,
  ziformula = ~spp
)
plot(simulateResiduals(m3))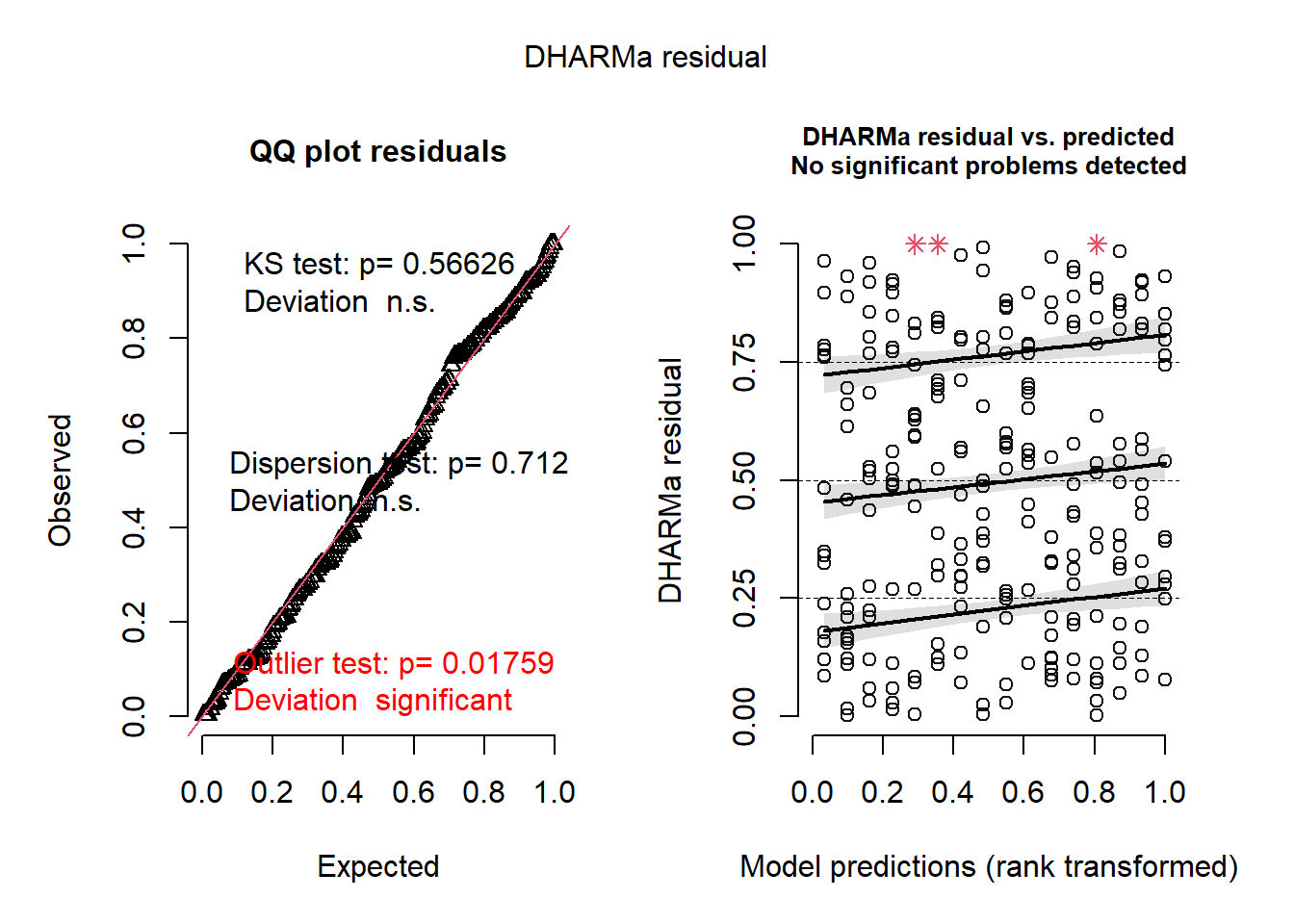

Code

m4 <- glmmTMB(
  ba_ha ~ treat * spp + (1 | site / treat),
  regen_pa,
  family = ziGamma(link = "log"),
  dispformula = ~ spp + treat,
  ziformula = ~spp
)
res4 <- simulateResiduals(m4)
plot(res4)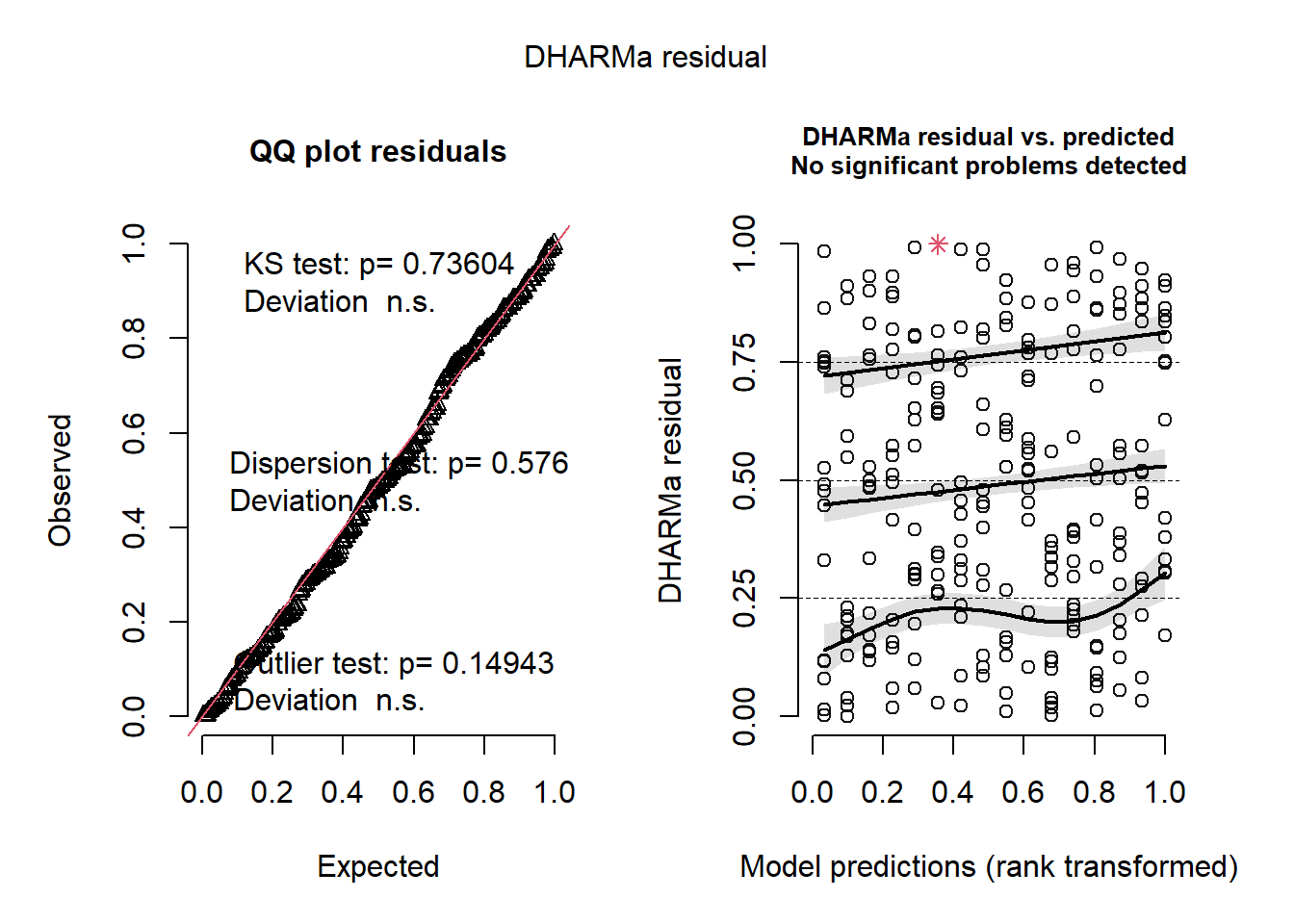

Code

plotResiduals(res4, form = regen_pa$spp)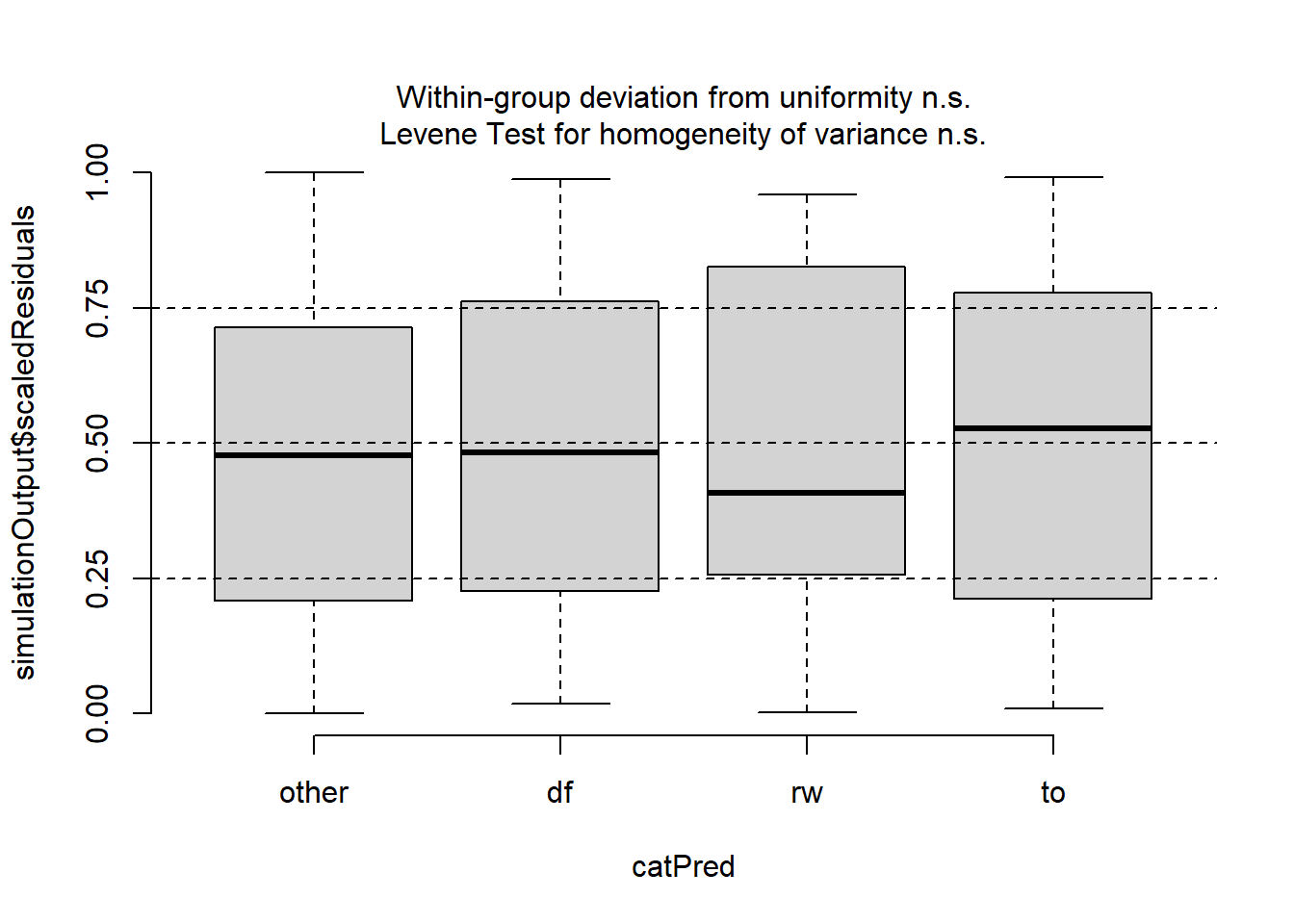

Code

plotResiduals(res4, form = regen_pa$treat)

Code

plotResiduals(res4, form = interaction(regen_pa$treat, regen_pa$spp))

Code

m5 <- glmmTMB(
  ba_ha ~ treat * spp + (1 | site:spp),
  regen_pa,
  family = ziGamma(link = "log"),
  dispformula = ~spp,
  ziformula = ~spp
)
plot(simulateResiduals(m5))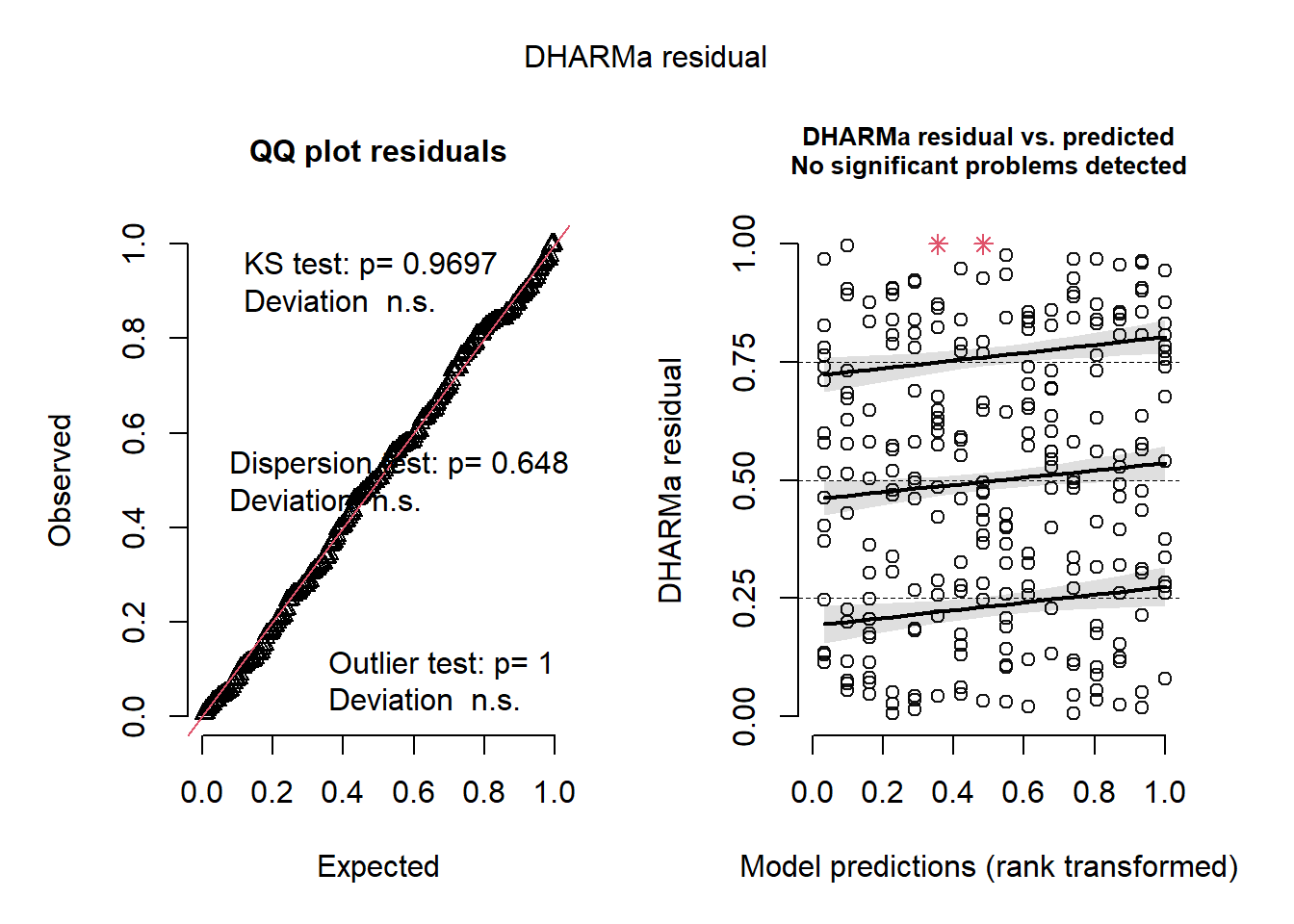

Code

m6 <- glmmTMB(
  ba_ha ~ treat * spp + (1 | site:spp) + (1 | site),
  regen_pa,
  family = ziGamma(link = "log"),
  dispformula = ~spp,
  ziformula = ~spp
)
plot(simulateResiduals(m6))

Code

m6a <- glmmTMB(
  ba_ha ~ treat * spp + (1 | site:spp) + (1 | site) + (1 | spp),
  regen_pa,
  family = ziGamma(link = "log"),
  dispformula = ~spp,
  ziformula = ~spp
)
plot(simulateResiduals(m6))

m7 <- glmmTMB(
  ba_ha ~ treat * spp + (1 | site),
  regen_pa,
  family = ziGamma(link = "log"),
  dispformula = ~spp,
  ziformula = ~spp
)
plot(simulateResiduals(m7))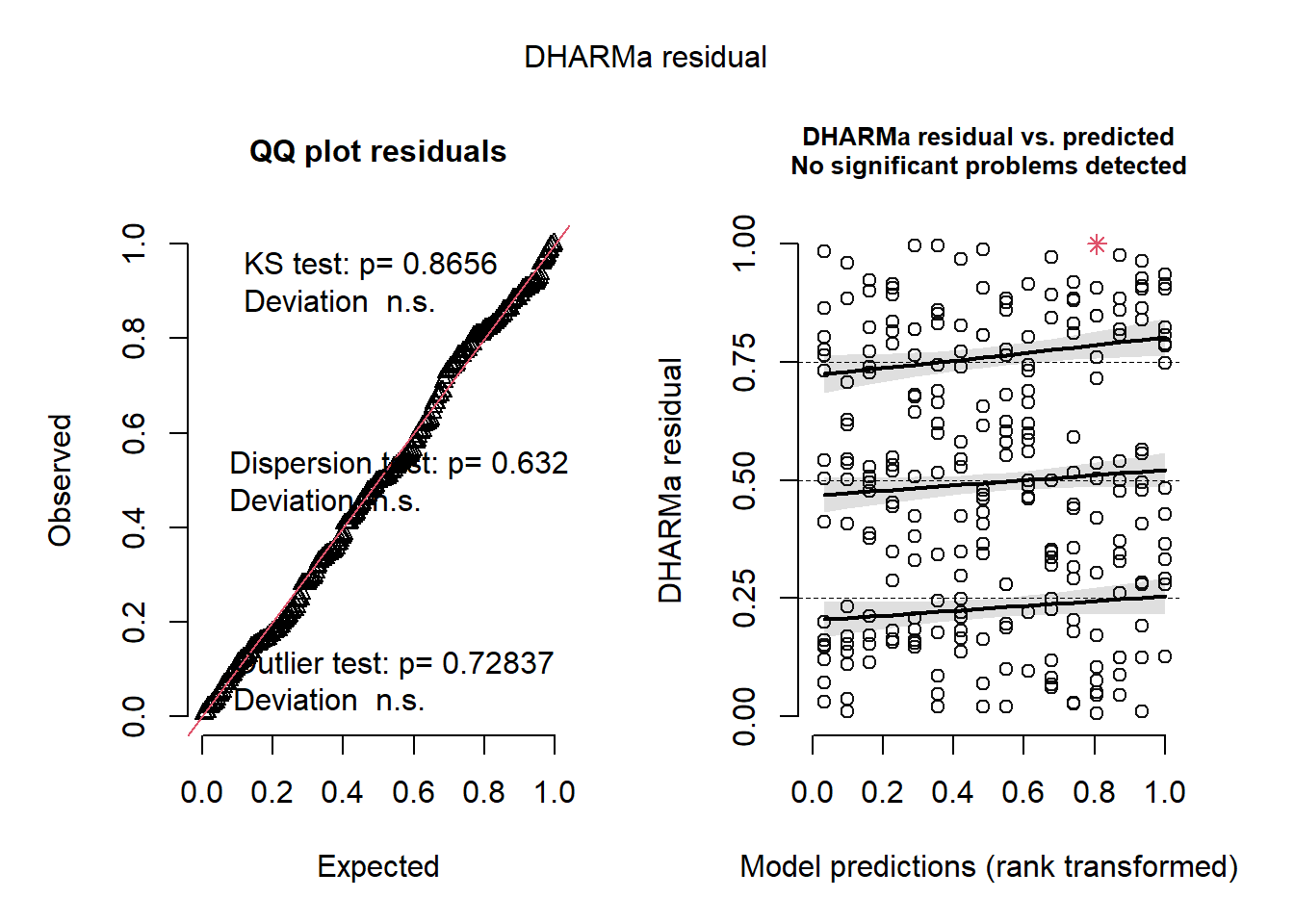

Code

AIC(m1, m2, m3, m4, m5, m6, m6a, m7)

    df       AIC
m1  20 1408.0527
m2  22  848.3301
m3  26  647.9944
m4  29  649.8549
m5  25  642.8537
m6  26  644.3800
m6a 27  646.3800
m7  25  645.9944

Code

# vectorized function to calculate rmse from predicted and actual values for any
# number of models provided as arguments. Models must have model.frame and
# predict methods.
# Output is a data frame with columns "model" and "rmse".
#' @param ... models to calculate rmse for
#' @return data frame with columns "model" and "rmse"
rmse <- function(...) {
  dots <- substitute(list(...))[-1]
  arg_strings <- vapply(dots, deparse, character(1))
  models <- list(...)
  rmse <- sapply(models, function(model) {
    actual <- model.response(model.frame(model))
    pred <- predict(model)
    sqrt(mean((pred - actual)^2))
  })
  rmse
  arg_strings
  data.frame(model = arg_strings, rmse = rmse)
}

rmse(m1, m2, m3, m4, m5, m6, m6a, m7)

  model     rmse
1    m1 3.464773
2    m2 3.511133
3    m3 4.385219
4    m4 4.385410
5    m5 4.378418
6    m6 4.379542
7   m6a 4.379542
8    m7 4.385218

Code

AIC(m1, m2, m3, m4, m5, m6, m6a, m7)

    df       AIC
m1  20 1408.0527
m2  22  848.3301
m3  26  647.9944
m4  29  649.8549
m5  25  642.8537
m6  26  644.3800
m6a 27  646.3800
m7  25  645.9944

Select this model

Code

mba <- m5

This model is the simplest, has the lowest AIC and has well-behaved residuals.

Here I plot some simulations from this model to see if it generates plausible data.

Code

regen_pa |>
  mutate(simulate(mba, nsim = 5)) |>
  rename(obs = ba_ha) |>
  pivot_longer(where(is.double), names_to = "type", values_to = "ba_ha") |>
  ggplot(aes(
    treat,
    ba_ha,
    group = interaction(type, treat),
    fill = forcats::fct_collapse(type, sim = paste0("sim_", 1:5))
  )) +
  geom_boxplot() +
  facet_wrap(~spp, scales = "free_y") +
  labs(fill = "obs/sim")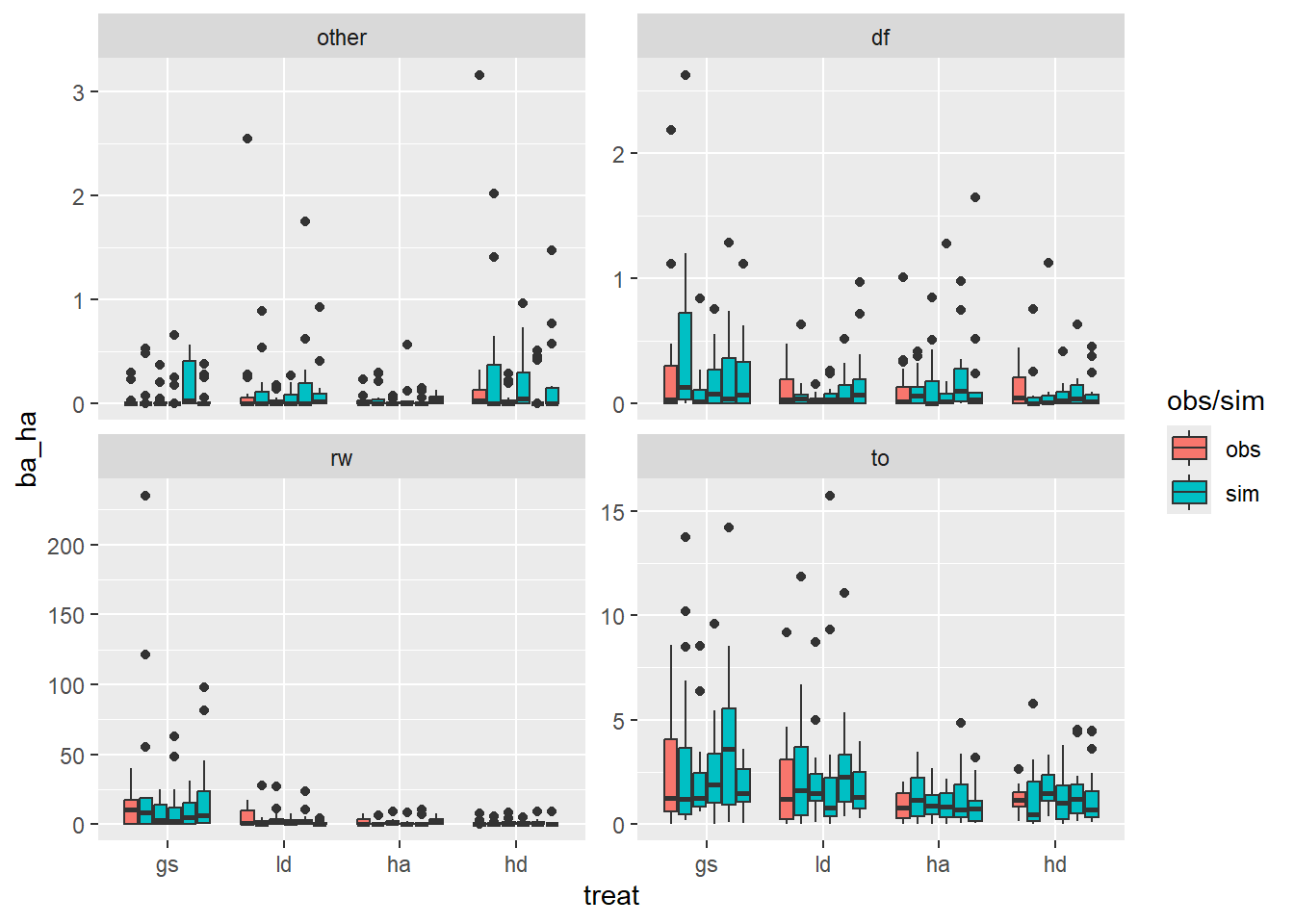

Finally, significant differences?

Code

avg_predictions(
  mba,
  newdata = datagrid(treat = unique, spp = unique, site = unique),
  by = c("spp", "treat"),
  re.form = NULL
) |>
  ggplot(aes(treat, estimate)) +
  facet_wrap(~spp, scales = "free", labeller = plot_labels) +
  geom_linerange(
    aes(ymin = conf.low, ymax = conf.high),
    color = "gray70",
    linewidth = 2.3,
    show.legend = FALSE
  ) +
  geom_point(color = "black", size = 2) +
  labs(x = "Treatment", y = expression(Basal ~ Area ~ (m^2 %.% ha^-1))) +
  scale_x_discrete(labels = toupper)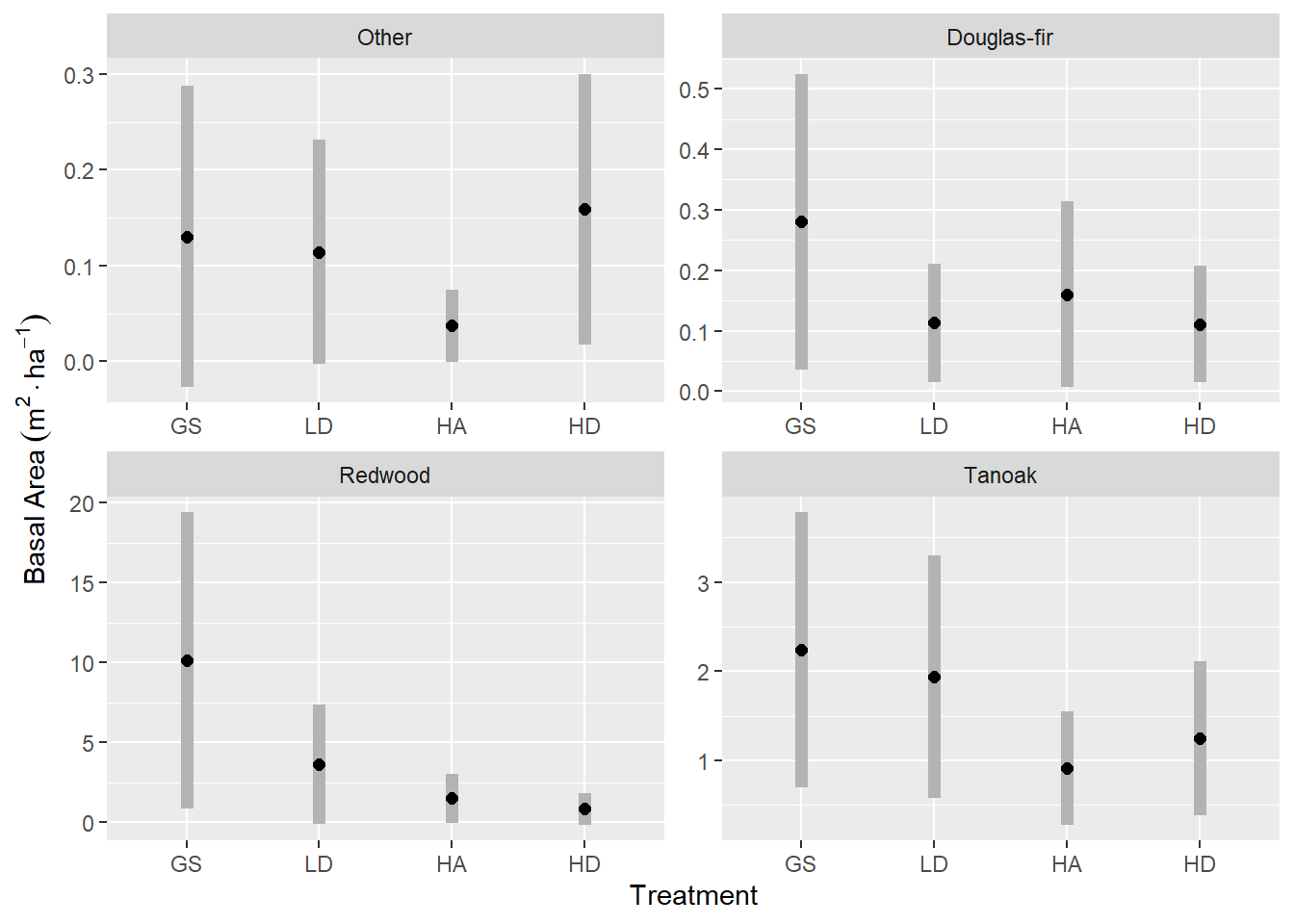

Here are the (would be) most significant contrasts between treatment, within species.

Code

comparisons(
  mba,
  newdata = datagrid(treat = unique, spp = unique, site = unique),
  variables = list(treat = "pairwise"),
  by = "spp",
  re.form = NULL,
) |>
  as_tibble() |>
  group_by(spp) |>
  mutate(p.adjust = p.adjust(p.value)) |>
  filter(p.value <= 0.1) |>
  select(-c(term, s.value)) |>
  tinytable::tt() |>
  tinytable::format_tt(digits = 2, num_fmt = "decimal")

contrast	spp	estimate	std.error	statistic	p.value	conf.low	conf.high	p.adjust
hd - ha	other	0.12	0.07	1.83	0.07	-0.01	0.25	0.4
ha - gs	rw	-8.61	4.56	-1.89	0.06	-17.55	0.34	0.3
hd - gs	rw	-9.28	4.64	-2	0.05	-18.38	-0.18	0.27
ha - gs	to	-1.33	0.65	-2.03	0.04	-2.61	-0.05	0.25
ha - ld	to	-1.02	0.58	-1.76	0.08	-2.15	0.11	0.39

13.1 Douglas-fir counts

For Douglas-fir in particular, we are interested in the counts of stems more than the basal area. This, requires another model. A counts model.

Here’s the raw counts. There doesn’t appear to be any treatment differences in the number of Douglas-fir seedlings per plot.

Code

regen_df <- regen |>
  count(site, treat, plot, spp) |>
  complete(nesting(site, treat, plot), spp, fill = list(n = 0)) |>
  filter(spp == "df")

regen_df |>
  ggplot(aes(treat, n * per_ha["corner"])) +
  geom_boxplot() +
  labs(x = "Treatment", y = expression(Stems %.% ha^-1))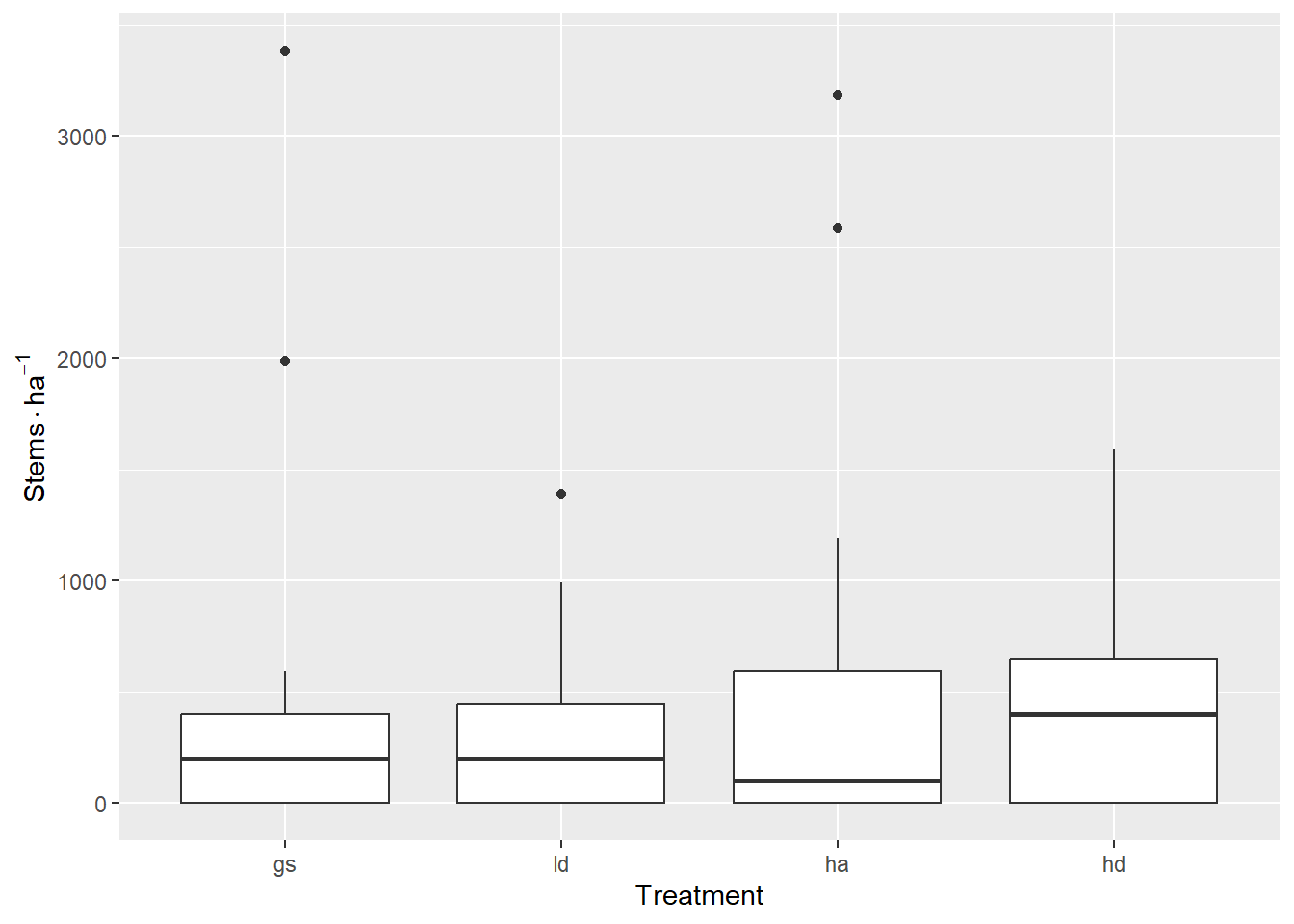

Figure 13.2: Summary of raw count data for Douglas-fir expressed in stems per hectare, for Douglas-fir seedlings in four harvest treatments 10 years after harvest.

A negative binomial model seems to fit acceptably when modeling raw counts (not TPH). I was not able to achieve model convergence with the specification of zero inflation or dispersion formulae.

Code

m1 <- glmmTMB(
  n ~ treat + (1 | site) + (1 | site:treat),
  regen_df,
  family = nbinom1()
)


res1 <- simulateResiduals(m1)
plot(res1)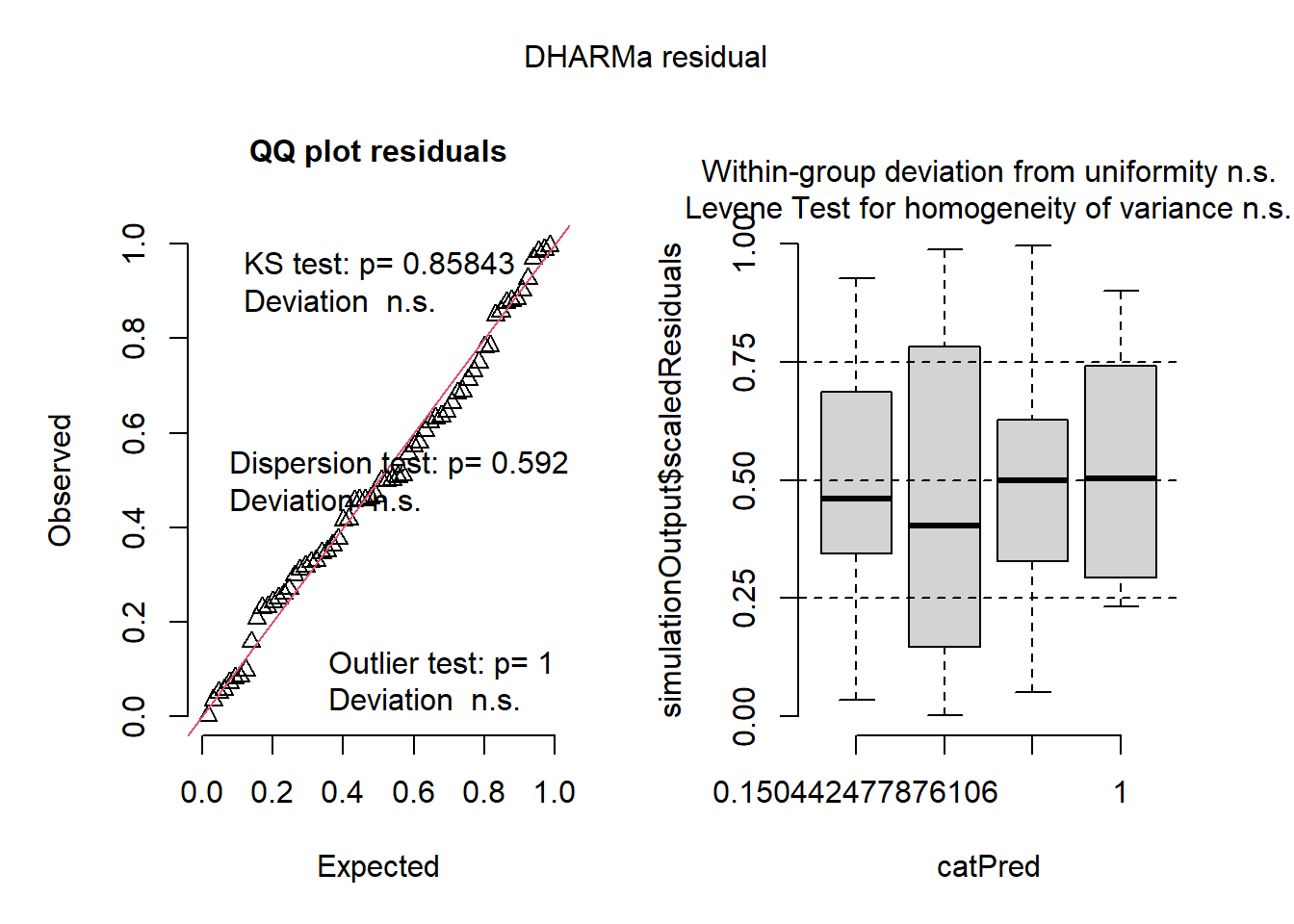

Select this model

Code

mdf <- m1

There are no statistically detectable differences

Code

emmeans(m1, "treat")

 treat emmean    SE  df asymp.LCL asymp.UCL
 gs     0.704 0.416 Inf    -0.111      1.52
 ld     0.509 0.433 Inf    -0.340      1.36
 ha     0.608 0.434 Inf    -0.242      1.46
 hd     0.983 0.390 Inf     0.219      1.75

Results are given on the log (not the response) scale. 
Confidence level used: 0.95

The model for Douglas-fir seedling counts does not result in any statistically significant differences between treatments. Generally, we expect about six seedlings per 4-meter-radius plot, or 1,000 to 1,400 seedling per hectare.

Code

emmeans(m1, "treat") |>
  contrast("pairwise") |>
  as_tibble() |>
  tinytable::tt()

Table 13.1: P-values for pairwise contrasts of Douglas-fir seedling counts in in four different harvest treatments 10 years after harvest.

contrast	estimate	SE	df	z.ratio	p.value
gs - ld	0.19546011	0.4004914	Inf	0.4880507	0.9617809
gs - ha	0.09613691	0.4132590	Inf	0.2326311	0.9955689
gs - hd	-0.27803131	0.3680676	Inf	-0.7553812	0.8743937
ld - ha	-0.09932320	0.4261828	Inf	-0.2330531	0.9955450
ld - hd	-0.47349142	0.3842515	Inf	-1.2322436	0.6062714
ha - hd	-0.37416822	0.3949796	Inf	-0.9473103	0.7792439

Save data from this page for future use

Code

save(
  regen,
  spp_col,
  per_ha,
  for_const,
  mba,
  regen_pa,
  mdf,
  regen_df,
  file = "regen_visualize.rda"
)